Performance Analysis of Outage Probability and Error Rate of Square M-QAM in Mobile Wireless Communication Systems over Generalized α-μ Fading Channels with Non-Gaussian Noise

Fares S. Almehmadi, Osamah S. Badarneh

University of Tabuk, Electrical Engineering Department, Tabuk, 71491, Saudi Arabia

I. INTRODUCTION

The Generalized Gaussian distribution (GDD)is a general noise distribution used to model additive noise in several communication systems [1, 2, and the references therein]. The beauty of the GGD lies in its generality as it includes different types of noises, such as the Gaussian noise, impulsive noise, Laplacian noise, and uniform noise. The aforementioned noises exist in several applications. Some of these applications are: underwater acoustic communication, spectrum sensing, multi-user interference in ultra-wide-band, wireless and power-line communications, co-channel and adjacent channel interference in mobile cellular systems.

Over the past few years, the performance of different modulation schemes in static communication systems over various fading channels in non-Gaussian environments has been investigated. Wanget al.proposed a novel closedform symbol error rate (SER) expression for orthogonal space-time block coded (OSTBC)orthogonal frequency division multiplexing(OFDM) systems over Nakagami-mfading channels [3]. The results demonstrated that the derived SER expression perfectly captures the performance of the OSTBC-OFDM systems under different antenna configurations, various modulation schemes, and various fading conditions. The authors in [4] analyzed the performance of discrete-rate adaptive modulation (AM) scheme for distributed antenna system (DAS) with imperfect channel state information. The analysis is based on the variable switching threshold (VST) by utilizing the maximum a posteriori method. In [5], a new technique to handle the problem of error propagation in a conventional multi-hop decode-and-forward system was proposed. The proposed technique employs a log likelihood ratio (LLR) modier at destination to correct the LLRs before sending them to the forward error correction (FEC) decoder. The authors in [6], investigated the bit error rate (BER)performance of physical-layer network coding(PNC) in asymmetric two-way relay channels for different asymmetric cases. The analytical and simulation results showed that uplink asymmetry and node asymmetry have the worst BER performance among other asymmetric cases. Yonget al.presented a new nonline-of-sight (NLOS) channel to accurately model the turbulence-induced scintillation attenuation (SA) [7]. Based on this channel model, the BER performance during turbulence of the NLOS ultraviolet (UV) communication system with On-Off Keying (OOK)modulation and Maximum Likelihood (ML)detection was analyzed. The authors in [8, 9]derived closed-form expressions for the SER ofM-ary phase shift keying (M-PSK) inα-η-μand extended generalized-K(EGK) fading channels subject to additive Laplacian noise,respectively. Banerjee and Agrawal derived analytical expressions for error probability of binary PSK, quadrature PSK, andM-ary pulse amplitude modulation (M-PAM) constellations in an underwater acoustic system in the presence of non-Gaussian noise [10]. The authors in [11], presented a novel goodnessof-fit detection scheme for spectrum sensing over the generalized Gaussian noise channel.Lower- and upper-bound expressions for SER for generic signal constellations impaired by additive isotropic generalized Gaussian noise assuming a minimum distance detector were derived and evaluated in [12]. Souryet al.investigated the performance of the average symbol error probability (SEP) of PAM and quadrature amplitude modulation (QAM)constellations over the EGK fading channels subject to additive white generalized Gaussian noise (AWGGN) [13]. The authors in [14],analyzed the BER performance of coherent binary modulation schemes using the moment generating function approach in static wireless systems over theα-μfading channels with additive white Gaussian noise (AWGN).The performance of adaptive modulation with selection combining (SC) for different transmission schemes overα-μfading channels was investigated in [15]. Soodet al.studied the BER performance of BPSK and QPSK for orthogonal frequency division multiplexing(OFDM) systems inα-μfading channels[16]. However, the above works consider only static networks. In the literature, there are a few works that take into consideration the mobility effect on the performance of the wireless communication systems [17, 18].

To the best of authors’ knowledge, the performance of squareM-QAM signaling in mobile networks over theα-μfading channels impaired by AWGGN has not been considered in the literature. To this end, in this letter, we obtain new and exact closed-form expressions for the average SER of squareM-QAM. The obtained expressions consider static and mobile receivers and they are valid for integer and non-integer values of the fading parametersαandμ.

The remainder of this paper is organized as follows. Section II describes the system and channel models. In Section III, the mathematical analysis for the average SER of squareM-QAM for the system under consideration is provided. Some representative numerical and simulation results are discussed in Section IV.Finally, Section V concludes this letter.

II. SYSTEM AND CHANNEL MODELS

In this paper, we consider a typical single-in-put single-output communication system,which can be modeled as

whereh∈?+is the channel fading envelope,gis the transmitted signal, andz∈? is an AWGGN with zero mean and varianceσ2. In this paper, we assume that the fading envelopehfollows theα-μfading distribution. Theα-μdistribution is proposed to model the small-scale variation of the fading signal. In addition, it is considered as a general distribution in the sense that it includes other wellknown fading channels as special cases, for example, the Nakagami-m(α=2,μ=m),the Weibull (μ=1), and the Rayleigh (α=2,μ=1) distributions. The pdf of the instantaneous received powerX(or, equivalently, the received SNR, since noise power is set to unity) can be written as [14]

whereα(α＞ 0) is an arbitrary parameter andrepresents the number of multi-path of the received signal, Γ(·) is the gamma function [19, Eq. (8.310.1)]. Heredenotes the average received power,whereris the propagation distance between the transmitter-receiver pair,δ(2≤δ≤5) is the path-loss exponent, andPtis the transmit power.

The pdf of the generalized Gaussian noise(GGN) in (1), with meanτand varianceσ2,can be dened as [20]

2.1 Static networks: outage probability analysis

In case of static networks, the propagation distanceris constant. Thus, the cdf of the received SNR in static networks (i.e.,r=D) can be obtained using (2) and [19, Eq.(3.381.8)], that is

1) Asymptotic Outage Probability Analysis:At low SNR, asymptotic expression for the outage probability can be derived using ( ef{cdfstatic}) asx→0. As such, One can obtain

2.2 Mobile networks: outage probability analysis

In mobile networks, the transmit power is constant whereas the propagation distance is a random variable because of the mobility of nodes. As such, the conditional pdf of the received signal power between the transmitter-receiver pair can be given as

The received power can be obtained by averaging (6) over the pdf of random distancer.In a realistic mobility scenario the range ofris 0≤r≤D[21], therefore

In this paper, and without loss of generality, the random way-point (RWP) mobility

model is considered. In this mobility model,the receiving nodes are located at randomly selected coordinate points in the service area,which depends on the network topology. For example, a 1D topology is modeled by a line,whereas a 2D topology is modeled by a circle, while a 3D topology is implemented by a sphere. In all network topologies, it is assumed that the transmitter is located at the origin. It is shown in [21] that the pdf of the distancer,between the transmitter-receiver pair, assuming a RWP mobility model can be given as

where parametersn,Biandβidepend on the number of dimensions considered in the network topology. For 1D topology:n=2,Bi=[6,?6],βi=[1,2], for 2D topology:n=3,whereas for 3D topology:n=3,

To obtain the pdf of the received powerone can substitute (6) and (8) into (7).That is

Using [19, Eq. (3.381.8)], then the unconditional distribution of the received power is readily obtained as

whereγ(·,·) is the lower incomplete gamma function [19, Eq.(8.350.1)].

The cdf of the received SNR can be found,viawith the help of (10)and [22, Eq. (1.2.1.1)] as

Note that (11) can be used to study the outage performance in mobile networks, whereis a predened threshold.

1) Asymptotic Outage Probability Analysis:At low SNR, asymptotic expression for the outage probability can be derived using (11)asx→0. As such, we obtain (12) after some mathematical manipulations

III. ANALYSIS OF SER FOR SQUARE M-QAM

The conditional SER for squareM-QAM,SER, in AWGGN environment assuming a received SNRxcan be written as

3.1 Static networks

The average SER in static networks can be obtained by substituting (2) and (3) into (15). As such, one obtains

and

The integral Φsin (17) can be solved using[25, Eq. (2.25.1.1)] and [25, Eq. (8.3.2.7)],after representing the exponential function in terms of FHF using [24, Eq. (1.125)] and then using (14), as

Note that (19) can be rewritten in terms of Meijer’s G-function with the help of [25, Eq.(8.3.2.22)] as in (20), on the top of the next page, whereis rational in (20) (with gcd(?,k)=1), in the bottom at this page. It is worth mentioning that the Meijer’s G-function is a built-in function in the most of wellknown software packages such as MATLAB and MATHEMATICA.

The integral Ψsin (21) can be solved in terms of the bivariate Fox’s H-function(BFHF) using [26, Eq. (2.3)]. The results is shown in (21), in the bottom at this page.

1) Asymptotic SER Analysis:At high SNR,the second term in (16) can be neglected.Thus, the asymptotic expression for the average SER can be expressed as

where ΦsAsycan be obtained using Φsin (19),with the help of [27, Eq. (1.8.4)], and after some algebraic manipulations as

Now, substituting (23) back into (22), then the asymptotic average SER can be obtained as

3.2 Mobile networks

In case of mobility, the average SER can be derived by plugging (10) and (13) into (15),that is

whereby

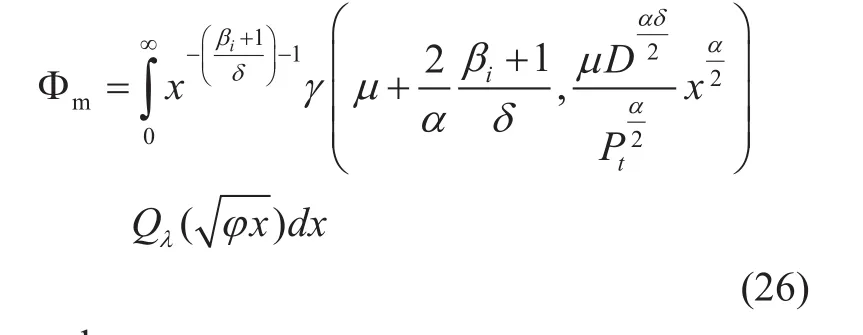
and

The integrals Φmand Ψmcan be solved by, first, representing the lower incomplete gamma function in terms of FHF by sequentially applying [25, Eq. (8.4.16.1)], [25, Eq.(8.3.2.21)], and [24, Eq. (1.59)]. After that,we obtain the final results for Φmas in (28)and Ψmas in (30) with the help of [25,Eq.(2.25.1.1)] and [26, Eq. (2.3)], respectively. Note that (28) can be rewritten in terms of Meijer’s G-function as in (29).

1) Asymptotic SER Analysis:At high SNR,the asymptotic average SER can be written as

where ΦmAsycan be obtained using Φmin (28),with the help of [27, Eq. (1.5.9)], and after some algebraic manipulations as

Plugging (32) back into (31) and after simple mathematical manipulations, thus the asymptotic average SER is expressed as

Fig. 1. Outage probability versus Pt in α-μ fading channel for 1D network with γth=2, α=3.5, μ=1.5, and δ=3.

IV. RESULTS AND DISCUSSION

This section investigates the impact of the mobility, noise shaping parameter, and fading parameters on the average SER. Please note that the FHF and BFHF can be accurately computed using the methods outlined in [28].

Figure 1 depicts the outage probability versus transmit powerPtin 1D mobile network over theα-μfading channels forγth=2,α=3.5,μ=1.5, andδ=3. The figure shows the effect of the distance on the outage probability performance. It is clear that as the distance between the transmitter-receiver pair decreases, the outage performance improves.This is because the average received power is inversely proportional to the distance. As such, as the distance decreases; thus the average received power increases and therefore the system performance improves. Also, thegure shows that the asymptotic analysis complies very well with the slope of the outage probability curves.

In figure 2, we depict the results of average SER for 16-QAM in a static network forD=100 m,δ=2,α=1.5, andμ=4.5 .Thegure shows the effect of the noise shaping parameterλon the system performance.The average SER curve withλ→∞ (i.e.,uniform noise) is provided as a benchmark for comparison. It can be seen that the system performance has different behaviors depending on the values ofλandPt. More precisely,one can note that the performance enhances asλdecreases. However, asPtincreases beyond a threshold value, the system performance enhances asλincreases. For example, whenλ=1/10 the system performance is better compared to the case whenλ=1/3. AsPtincreases beyond a threshold value (in this examplePt

thr?72 dB), the system performance is better whenλ=1/3. We have noticed similar behavior for different values ofα,μ,D,andδ.

Figure 3 plots the average SER performance for Gaussian and Laplacian noise in 1D network. Also, the figure shows that im-pact of the severity of fading parameters on the system performance. The results shows that as the fading parametersαand (or)μincrease(s), the SER improves. This is becauseμrepresents the number of multi-path in each clusters. As such, asμincreases the number of multi-path increases and therefore the received SNR improves, thus the SER improves. On the other hand, asαincreases the received SNR increases; and therefore the SER improves. This is becauseαrepresents the power exponent of the received SNR.Analytical results are validated through Monte-Carlo simulations. Both results are in good agreement, which veries the accuracy of our analysis.

V. CONCLUSION

In this paper, we derived exact closed-form expressions for the average SER of squareM-QAM over theα-μfading channels with AWGGN. The derived expressions consider static as well as mobile receivers. In addition,the obtained expressions are valid for integer and non-integer values of the fading parameters. The outage probability is also analyzed.The results showed that the system performance improves as the fading parametersαand(or)μincrease(s). On the other hand, as the path-loss exponent and(or) the distance between the transmitter-receiver pair decrease(s),the system performance improves. Also, the results demonstrated that at high values of transmit powerPt, the system performance improves as the noise shaping parameterλincreases. For future work, the performance of otherM-QAM constellations accompanied with power allocation techniques may be considered.

Fig. 2. Average SER of 16-QAM in static network over the α-μ fading channels under different types of noise.

Fig. 3. Average SER of 16-QAM in 1D network over the α-μ fading channels under Gaussian and Laplacian noises.

ACKNOWLEDGMENT

The authors gratefully acknowledge the sup-port of SNCS Research Center and the Deanship of Scientic Research at the University of Tabuk, Saudi Arabia for theirnancial and inkind support for the project no. S-1438-0161.

Fig. 4. Average SER of 64-QAM in 3D, 2D, and 1D networks over the α-μ fading channels under Laplacian noise.

[1] X. Yang, M. Li, and X. Zhao, “Optimum detectors of line spectrum signals in generalized Gaussian noise,” inProc. ICMTMA, 2011, pp. 819–822.

[2] N. C. Beaulieu, G. Bartoli, D. Marabissi, and R.Fantacci, “The structure and performance of an optimal continuous-time detector for Laplace noise,”IEEE Commun. Lett., vol. 17, no. 6, pp.1065–1068, 2013.

[3] X. Wang, N. Wu, and C. Gao, “Generalised closed-form symbol error rate analysis for orthogonal space-time block coded OFDM system,”China Communications, vol. 10, no. 9, pp.155–164, 2013.

[4] X. Yu, W. Tan, B. Wu, and Y. Li, “Discrete-rate adaptive modulation with variable threshold for distributed antenna system in the presence of imperfect CSI,”China Communications, vol.11, no. 13, pp. 31–39, 2014. [5] M. Tingting,W. Ning, Y. Hongwen, and Y. Dacheng, “BER modified decode-and-forward protocol for OFDM-based linear multihop networks,”China Communications, vol. 11, no. 11, pp. 34–43,2014.

[6] L. Bo, W. Gang, P. H. J. Chong, Y. Hongjuan, Y.Guan, and S. Xuejun, “Performance of physical-layer network coding in asymmetric twoway relay channels,”China Communications,vol. 10, no. 10, pp. 65–73, 2013. [7] Z. Yong,W. Jian, X. Houfei, and L. Jintong, “Non-line-ofsight ultraviolet communication performance in atmospheric turbulence,”China Communications, vol. 10, no. 11, pp. 52–57, 2013.

[8] O. S. Badarneh, “Error rate analysis of M-ary phase shift keying in α-η-μ fading channels subject to additive laplacian noise,”IEEE Commun. Lett., vol. 19, no. 7, pp. 1253–1256, 2015.

[9] H. Soury and M. Alouini, “Symbol error rate ofM-PSK over EGK channels perturbed by a dominant additive laplacian noise,”IEEE Trans. Commun., vol. 63, no. 7, pp. 2511–2523, 2015.

[10] S. Banerjee and M. Agrawal, “Underwater acoustic noise with generalized Gaussian statistics: Effects on error performance,” inProc.OCEANS- MTS/IEEE, 2013, pp. 1–8.

[11] S. Gurugopinath, R. Muralishankar, and H. N.Shankar, “Dierential entropy-driven spectrum sensing under generalized Gaussian noise,”IEEE Commun. Lett., vol. 20, no. 7, pp. 1321–1324,2016.

[12] B. Dulek, “Bounds on symbol error rate for additive isotropic generalised Gaussian noise channels,”Elect.Lett., vol. 50, no. 10, pp. 777–778, 2014.

[13] H. Soury, F. Yilmaz, and M.-S. Alouini, “Error rates ofM-PAM andM- QAM in generalized fading and generalized Gaussian noise environments,”IEEE Commun. Lett., vol. 17, no. 10, pp.1932–1935, 2013.

[14] A. M. Magableh and M. M. Matalgah, “Moment generating function of the generalized α-μ distribution with applications,”IEEE Commun. Lett., vol. 13, no. 6, pp. 411–413, 2009.

[15] A. Andrawes and R. Nordin, “Performance of adaptive modulation in alpha- mu fading channel under selection combining diversity,” inProc.TAFGEN, 2015, pp. 111–116.

[16] N. Sood, A. K. Sharma, and M. Uddin, “BER performance of OFDM-BPSK and -QPSK over generalized alpha-mu fading distribution,” inProc.IEEE IACC, 2009, pp. 1197–1199.

[17] V. A. Aalo, C. Mukasa, and G. P. Efthymoglou,“Effect of mobility on the outage and BER performances of digital transmissions over Nakagami-mfading channels,”IEEE Trans. Veh.Technol., vol. 65, no. 4, pp. 2715–2721, 2016.

[18] F. S. Almehmadi and O. S. Badarneh, “On the error rate of coherent binary modulation techniques in mobile communication systems over gen- eralized fading channels impaired by generalized Gaussian noise,”AEU- International Journal of Electronics and Communications, vol. 82, no. Supplement C, pp. 14–19,2017.

[19] I. S. Gradshteyn and I. M. Ryzhik,Table of Integrals, Series, and Products, 7th ed. Academic Press, California, 2007.

[20] A. Tesei and C. S. Regazzoni, “Use of fourth-order statistics in non- Gaussian noise modelling for signal detection: the generalized Gausian pdf in terms of kurtosis,” inProc. EUSIPCO-96,1996, pp. 1–4.

[21] K. Govindan, K. Zeng, and P. Mohapatra, “Probability density of the received power in mobile networks,”IEEE Trans. on Wireless Commun.,vol. 10, no. 11, pp. 3613–3619, 2011.

[22] A. P. Prudnikov, Y. A. Brychkov, and O. I.Marichev,Special Functions. Gordon & Breach Sci. Publ., New York, 1990, vol. 2.

[23] H. Soury, F. Yilmaz, and M.-S. Alouini, “Average bit error probability of binary coherent signaling over generalized fading channels subject to additive generalized gaussian noise,”IEEE Commun. Lett., vol. 16, no. 6, pp.785–788, 2012.

[24] A. Mathai, R. Saxena, and H. J. Haubold,The H-function theory applica- tions. Springer New York, 2010.

[25] A. P. Prudnikov, Y. A. Brychkov, and O. I. Marichev,Integrals, and Series: More Special Functions.Gordon & Breach Sci. Publ., New York, 1990,vol. 3.

[26] P. Mittal and K. Gupta, “An integral involving generalized function of two variables,”Indian Acad. Sci., pp. 117–123, 1972.

[27] A. Kilbas and M. Saigo,H-Transforms : Theory and Applications (Analyt- ical Method and Spe-cial Function), 1st ed. CRC Press, 2004.

[28] A. Soulimaniet al., “Performance analysis ofM-QAM multihop relaying over mmWave Weibull fading channels,”https://arxiv.org/abs/1610.08535, pp. 1–17, 2016.