State transfer on two-fold Cayley trees via quantum walks?

Xi-Ling Xue(薛希玲) and Yue Ruan(阮越)

School of Computer Science and Technology,Anhui University of Technology,Maanshan 243032,China

Keywords: perfect state transfer,two-fold Cayley tree,quantum walk

1. Introduction

Quantum walk is the quantum mechanical counterpart of classical random walk. There are two main types of quantum walk, namely the continuous-time quantum walk (CTQW)and the discrete-time quantum walk (DTQW), both of which have been shown to constitute a universal model of quantum computation.[1,2]Coined quantum walk(CQW)and scattering quantum walk (SQW) are two unitary equivalent DTQWs,[3]with the former defined on vertices and the latter on directed edges of the underlying graph. Quantum walks have been proven to be a useful framework in designing new quantum algorithms,such as search algorithms.[4–7]Another promising application is to perfectly transfer unknown quantum states between the source and target vertices of a graph.

Quantum state transfer within a quantum computer,which is an important task for quantum information processing, can be achieved by using a network of qubits, and such a network can be modelled mathematically by a graph. The problem of what graph structures lead to perfect state transfer(PST)has been of wide interest. State transfer is more important in network applications.[8–10]It has been extensively studied in various systems such as, hybrid solid-optomechanical interface,[11]optical microcavities,[12]and NMR system. It is also important as an effective way of routing as compared to other routing method.

As the addition of the coin states to the DTQW model leads to more difficult analytical solutions, most efforts to classify when perfect state transfer can occur have used the continuous-time model.[13–18]Chakraborty provided a protocol to achieve perfect state transfer for almost any graph.[19]There are two different approaches in the case of DTQW,namely,the transfer of a particle from one vertex to the other and the transfer of an arbitrary internal coin state, to the PST problem. In the first, the evolutionary operator is modified only at the source and target vertices. This method was analyzed on cycles in Ref. [20] and highly symmetric graphs in Refs. [21,22]. Typically, it does not allow for the transfer of the internal coin state of the particle. The second approach relies on defining dynamics at each individual vertex in order to achieve state transfer between two selected vertices.This method was analyzed in DTQWs on a circle[23–25]and a square lattice.[26]

The purpose of the work presented here is to investigate the state transfer problem on a two-fold Cayley tree between two roots using both CTQW and DTQWs. The Cayley tree has been widely used in solid state and statistical physics, as statistical mechanical models on it form a large class of exactly soluble models.[27,28]We find that the fidelity of the final state of the system and the target state in both the CTQW and the typical DTQW approach is less than unitary by analyzing the evolutionary process on the quotient graph of the two-fold Cayley tree. Instead,PST can be achieved by means of CQW with position-dependent nonrepeating coins and permutation coins in 2n time steps, where n is the generation of the twofold Cayley tree.

This paper is organized as follows. The relative definitions are provided in Section 2. In Section 3,we demonstrate the state transfer process via CTQW and SQW on the collapsed graph of the two-fold Cayley graph. Then we show how to use the nonrepeating coin to achieve PST in Section 4,We end with conclusion and discussion in Section 5.

2. Preliminaries

2.1. Perfect state transfer via quantum walks

We formalize the definition of perfect state transfer in the CTQW and DTQW scenarios below. Some of the definitions are taken from Refs.[29,30].

Let G(V,E) be a d-regular graph on which the walk is defined with adjacency matrix A=A(G). Given two vertices u and v of G,denote their respective characteristic vectors by euand ev. The matrix exp(iτA)represents a CTQW in G. We say that G admits perfect state transfer from vertex u to vertex v at a time τ if there is a complex number λ such that

exp(iτA)eu=λev.

Finding graphs that admit perfect state transfer is therefore translated into a problem that depends uniquely on the spectral properties of the matrix A.

The Hilbert space of CQW is HP?Hc. In the position space HP,a basis vector|v〉is associated with each of the vertices v,and in the coin space Hc,a basis vector|c〉is associated with each of the edges emanating from each vertex of G. The time evolution of a state vector is U =SF,where the shift operator

Here, v′is the vertex connected to v along the direction ci;and cjis the direction by which v′is connected back to v. ciand cjcorrespond to the edge-coloring scheme of G. If G is d-colorable, cjis typically chosen as cj=ci. As we will see in Subsection 3.2 that the two-fold Cayley trees are not d-colorable for the edges emanating from the middle vertices,cj/=cifor these vertices,meaning that a single edge is colored using two colors.

If the coin differs at different parts of the graph,the coin operator F takes the form

F =∑iPi?Ci,

where Piare projection operators such that ∑iPi=I (identity over HP) and Ciare unitary. If we are not concerned about whether the coin states are in the same configuration at vertex v′as they were at vertex v, perfect state transfer occurs between the two vertices after t steps if

The Hilbert space of SQW on graph G is spanned by all the directed edges states,where each edge corresponds to two states, one for each of the two possible directions. For each vertex k in G, there are two subspaces Akand Ωk, which are spanned by the outgoing and incoming edges of k, respectively. The local unitary operators act on vertex k as

where rkand tkare the reflection and transmission coefficients on vertex k,respectively to be chosen in such a way that Ukis unitary. The overall operator U describing one step of SQW on graph G is the combined action of all the local unitary evolutions. In the SQW scenario,perfect state transfer occurs between vertices v and v′after t steps if

where(v,w)∈E, (v′,w′)∈E, as both the two directed edges(v′,w′) and(w′,v′)are connected to the target vertex v′.

2.2. Nonrepeating quantum walk

Proctor et al. introduced two previously unstudied types of coin operators for the DTQW, one of which is the nonrepeating coin,[31]which we will use in our perfect state transfer scheme on two-fold Cayley trees. Nonrepeating coin is the most general SU(4)operator with zeros on the diagonal, and the complete form can be found in Ref. [31]. With the shift operator defined in Eq. (1), the coin never permits amplitude to move in the same direction in two consecutive steps. The specific nonrepeating coin we use is

It was shown that the nonrepeating walk has some notable properties,namely,the mean and standard deviations of the radial distance from the origin of the walker are independent of the choice of the initial condition,and the even-order joint moments of the nonrepeating walker are independent of the initial condition, being determined by five parameters derived from the coin instead.[31]

2.3. Two-fold Cayley tree

A tree in which each non-leaf graph vertex has a constant number of branches is called a Cayley tree, and a twofold Cayley tree is an extension of the Cayley tree. The construction of the two-fold Cayley tree is as following.[28]Start from two roots and 0′,as the central points of the graph. Then we add q=4 different points connected to each central point which may be named as the first shell. We call the set of these q points connected to the central point 0 the first left shell and that connected to the central point 0′the first right shell. Then each of these first shell points is joined to(q?1)new points.Therefore,in total,points of the first shell have q(q?1)nearest points which form the second shell. If we continue in this way, with the last step both the right and left (n ?1)thpoints connected to the same middle layer,the entire structure of the two-fold Cayley tree is formed.

In short, the two-fold Cayley tree graph with generation n and coordination number q is constructed by joining two open Cayley trees each containing n?1 shells at their boundaries by adding small polygons to ensure that all sites have the same coordination number q. A typical two-fold Cayley tree graph for the generation n=2 and coordination number q=4 is shown in Fig.1.

Fig.1.A two-fold Cayley graph with generation n=2 and coordination number q=4. Vertices in different layers are colored differently.

3. Failure of perfect state transfer using CTQW and SQW

We will consider state transfer on two-fold Cayley trees between two roots via CTQW and SQW schema respectively.In both cases,we determine the invariant subspace of the evolution operator of the walk,which is analogous to the analysis of CTQW algorithms[7]and SQW algorithms[6]on symmetric graphs. According to Theorem 1 in Ref.[14],the state transfer process on the quotient graph shares the same properties with that on its original graph. Since the distance between the source and the target vertices in two-fold Cayley trees depends on the diameter of the tree, so does the dimension of the invariant subspace. The dimensional reduction due to the symmetry of the graph greatly facilitates the analyzation of the evolutionary process.

3.1. State transfer using CTQW

The Hamiltonian in the above 5D basis is

where the second item in the first row, for example, is from the adjacency matrix,and it is 1/2 to convert between the normalizations of |p1〉 and |p2〉 times the 4 yellow vertices that connect to vertex 0. The eigen spectrum of the above Hamiltonian is

Two-fold Cayley trees have mirror symmetry, by which it means that the graph is identical from the points of view of vertexes 0 and 0′. A necessary condition for a mirror symmetric graph to admit PST, as is shown in Ref. [32], is that the ratios of differences of the eigenvalues of the Hamiltonian must be rational. That is,

where Q denotes the set of rational numbers. Given the set of eigenvalues of the Hamiltonian, it can easily be verified that the two-fold Cayley tree with generation n=2 and coordination number q=4 does not admit perfect state transfer. In fact,the Hamiltonian for the two-fold Cayley tree with generation n and coordination number 4 can be expressed as

The diagonal entrances of H are all 0 except for Hn+1,n+1,which is 2. Though it is impossible to obtain the whole eigenvalue set of the above Jacobi matrix, it is obvious that H has an eigenstate

associated with the integer eigenvalue θ =4,and our simulation results show that it has irrational eigenvalues for all n ≤5.We will then consider the general case for arbitrary n.

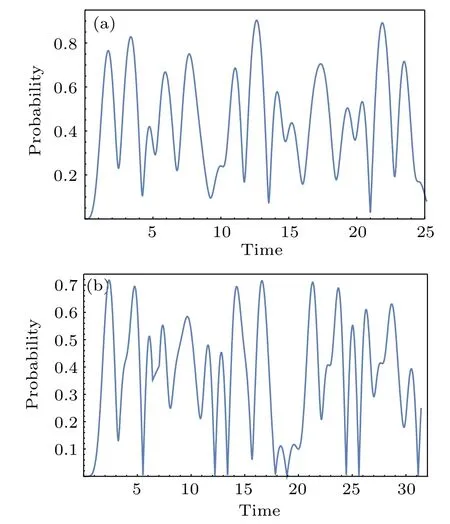
Fig.2. Fidelity for CTQW on two-fold Cayley trees as a function of time: (a)n=2;(b)n=3.

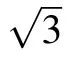
The two initial conditions are

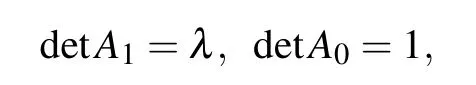
where the second condition is chosen so as to stay in agreement with the recurrence relation(indeed,detA2=λ detA1?4detA0=λ2?4).As shown in Ref.[34],though the eigenvalues λ can be expressed as a nonlinear equation in terms of the eigenvalues of the transfer matrix using the Cayley–Hamilton theorem, the solutions cannot be obtained analytically. It is obvious that the coefficients of the polynomial are all integers,and the coefficient of λ2n+1is 1. Thus,the characteristic polynomial of H is an integral coefficient monic polynomial.Gauss’lemma for monic polynomials tells us that the root λ is either an integer or irrational. The two-fold Cayley tree is,to the best of our knowledge,not an integral graph,meaning that the spectrum of its adjacency matrix does not consist entirely of integers.Equivalently,there must be some eigenvalues of H that are irrational.According to Ref.[32],the two-fold Cayley tree with coordination number 4 and generation n ≥2 does not admit perfect state transfer.

It should be noted that here the problem is converted into PST on an odd-length irrational-weighted path with a loop(potential) at the middle vertex. A most recent related study also gives a negative result for rational-weighted paths with or without potentials.[35]

3.2. State transfer via SQW

We consider the SQW search algorithm approach to the problem as in Refs. [21,22]. The reflection and transmission coefficients rkand tkin Eq. (2) are defined as follows. If k is one of the root vertices, rk=?1, tk=0. For all the other vertices, rk=?1/2, tk=1/2. This choice of local unitary operators is analogous to the choice of diffusive operator in Grover’s algorithm.[36]

Denote the directed edges of the original graph as(pi,pj)if they start from vertices in piand point to vertices in pj.Taking equal superpositions of identically evolving edges as orthonormal basis states,we define the following edge states:

The above states{|ψ1〉,|ψ2〉,...,|ψ9〉}correspond to the 9 directed edges of the collapsed graph. These states form a subspace of the Hilbert space, which we will see is invariant under the action of the unitary operator. We start the process from v0, with the coin states being the equal superposition of all the four directions pointing to the first left shell. That is,|ψstart〉=|ψ1〉.

As p1and p5are the source and target vertices, respectively, U|ψ2〉=?|ψ1〉, U|ψ8〉=?|ψ9〉. The local unitary operator on the other vertices in the collapsed graph can be obtained by considering the effect of the Grover diffusion operator as in Ref. [6]. In the basis {|ψ1〉,|ψ2〉,...,|ψ9〉}, the unitary operator U on the subspace can be expressed as

The state of the walk after t steps is given by |ψt〉 =Ut|ψstart〉. For illustration we display in Fig.3(a) the fidelity between the state of the walk and the target state as a function of the number of steps, which is given by f =|〈ψt|ψ8〉|2+|〈ψt|ψ9〉|2.Figure 3(b)plots the results on twofold Cayley trees with n=3. The fidelity is lower than the CTQW case,and in both cases it decreases as n increases.

Fig.3. Fidelity between the state of the walk after time t and the target state for the walk two-fold Cayley trees as a function of the number of steps t: (a)n=2;(b)n=3.

4. Perfect state transfer using nonrepeating coin

In this section we use a variation of the DTQW,the nonrepeating quantum walk,and find that PST can be achieved on two-fold Cayley trees between two roots.

A regular, undirected graph with N vertices of degree d is considered d-colorable if the edges incident on every vertex can be numbered 1 through d such that every edge between two vertices has the same number at either end. Though the Cayley trees are 4-colorable, the joined two-fold Cayley tree is not 4-colorable on the middle layer. The edges incident on the middle layer vertices could not be labeled with a single color between two successive walk steps. The detailed coloring scheme shown in Fig.4 is as follows. The three edges of each triangle in the middle layer are colored using the same set of colors as the edges connecting to their left parent,with the condition that the colors of the edges emanating from each vertex are distinct. All the three outgoing edges that connect the triangle to their right parent are colored with the remaining one color. These edges are not properly colored from the point of view of the right parent. In order to proceed on the CQW,they need to be recolored as the outgoing edges of the right parent. This is the case when ci/=cjin Eq.(1). To ensure all the amplitudes on these edges are collected in the following algorithm,each of these three edges is recolored with the same color as the edge that connects the triangle to its left parent.

The four colors of the edges are denoted from 1 to 4, so the edge with color i is denoted as ci, i=1,2,3,4. For the convenience of description, the vertices in the middle layer are labeled by their adjacent vertices in the left shell and the edge connecting them, and the primes stand for the vertices from the right Cayley tree.

Fig.4. The coloring scheme of two-fold Cayley tree with n=2 and q=4.

We start from the left root v0,with the coin state being in equal superposition of all the four edge states

The whole procedure can be divided into three parts. First the amplitude is scattered among all the vertices in the left side of the two-fold Cayley tree through nonrepeating walk. Then the scattered amplitude is swapped to the right side,using different permutation operators as coin operators at each vertex.At last, all the amplitudes are collected using the reverse of nonrepeating coin.

Step 1Apply SF1on the initial state,we get

The state after applying SF2is

Step 2Permutation coin operators are chosen according to each vertex to avoid amplitudes propagating among the middle layer vertices. For example,the permutation operator T1,2is used on the coin space of v12. Then the shift operator shifts the vertices to the right shell along the recolored edges

Step 3The recoloring scheme ensures that the amplitudes will be collected after another application of SF4,

The system now is in the target state with unitary probability. With another application of coin operator F5, the coin state will be in an equal superposition of the four edge states,the same with that in the initial state,

Thus, we can transfer the state with unitary fidelity using time steps that are the distance between the two roots.This scheme will work whatever the generation of the two-fold Cayley tree is, with proper permutation matrices to swap the amplitudes across the middle layer. And arbitrary coin state|ψC〉=a|c1〉+b|c2〉+c|c3〉+d|c4〉,with|a|2+|b|2+|c|2+|d|2=1,can be used as the initial coin state,which conforms with Ref.[31]that the transfer fidelity does not depend on the initial coin state.

5. Discussion and conclusion

We design algorithms using local non-reversal and permutation coin operators of a DTQW, which leads to perfect state transfer between two roots on a two-fold Cayley tree in time steps scaling as the distance covering them.In this model,the transfer of the internal coin state is also possible. Here we offer an application of the nonrepeating walk, with which a perfect state transfer is achieved while both CTQW and the typical DTQW approaches fail.

In the case of CTQW, for a natural choice of a timeindependent Hamiltonian, the evolution of a state of the network of qubits depends uniquely on the spectral properties of the adjacency matrix of the underlying graph. DTQW using position-dependent coins offers a greater possibility of control over the transport than is allowed in the CTQW case,since due to the extra degree of freedom one gains more control over the walk than is allowed in a standard continuous-time scenario.It agrees with the argument that there is a possibility that a discrete-time method is more powerful than the continuoustime counterpart.[32]

The ability of a specialized coin to perform perfect state transfer in a few steps on the two-fold Cayley tree adds another tool to the arsenal of DTQW,and what other coins may contribute to the state transfer on various graphs deserves to be further explored. On the other hand,given the above example of application of the nonreversal walk, whether there is any interesting application of the nonrepeating coin in Ref.[31]is a question worth studying.