Spin-orbit-coupled spin-1 Bose-Einstein condensates confined in radially periodic potential?
Ji Li(李吉), Tianchen He(何天琛),?, Jing Bai(白晶), Bin Liu(劉斌), and Huan-Yu Wang(王寰宇)
1Department of Physics,Taiyuan Normal University,Jinzhong 030619,China
2Basic Teaching Department,Shanxi Institute of Energy,Jinzhong 030600,China
3Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
Keywords: the spinor Bose-Einstein condensates,spin-orbit coupling,radially periodic potential
1. Introduction
The spins of the alkali-metal atoms are essentially free in an optical trap, which provides the possibility of studying condensates with a spin degree of freedom, the spinor Bose-Einstein condensates (BECs).[1-3]Spinor BECs have a new feature in which the order parameter is a vector rather than scalar quantity, which offers an ideal platform for probing many interesting topological excitations.[4-16]In terms of the interatomic interactions, one can observe matter-wave solitons in BECs.[6]Some researchers discussed the properties of quantum spin vortices in spinor BECs.[7-9]For the spinor BECs with rotation, it is found that there are coreless vortex, axisymmetric vortex, and nonaxisymmetric vortex in the system.[10,11]Mizushima et al. found singular vortex-lattice phases in rotating ferromagnetic BECs.[12]During dynamics of rotating spinor BECs, Ji et al. studied fractionalized half-quantum vortices in theory.[13]Subsequently, Seo et al. observed fractionalized half-quantum vortices in experiment.[14,15]In Rabi-coupled spinor BECs, the ground state can support skyrmionic vortex lattices.[16]In recent years, the research of spin-orbit(SO)coupling has been widely concerned in the field of condensed matter. However,the SO coupling is only slightly adjustable in materials due to the limitation of its own material parameters.The SO coupling in BECs can be controlled and tuned by using optical fields or a sequence of pulsed homogeneous magnetic fields.[17-29]The recent realization of SO coupling in BECs,owing to coupling between the spin and the center-of-mass motion of the atom,provides more possibilities to explore exotic novel quantum states.[30-36]Wang et al. found that SO coupling can induce plane wave and density stripe phases in BECs without external potential.[30]If the external potential is considered, new topological excitations will appear in the system,such as halfskyrmion,[31]fractionalized vortices,[32]skyrmion lattice,[33]the monopoles with the polar-core vortex.[34]In addition,the SO coupling can lead to the appearances of quantum quasicrystals in dipolar condensates.[36]
Recently, the impact of SO coupling on BECs in ringshaped potentials has attracted considerable interest, due to the persistent flow states and symmetry-breaking phenomena being found.[37-43]Zhang et al. studied the ground state properties of two-component SO-coupled BECs in a toroidal trap and showed that the system exhibits a modified stripe, an alternately arranged stripe,and countercircling states.[40]Wang et al. further discussed ground state phases of the SO-coupled spinor BECs in the toroidal trap.[43]Especially intriguing is the impact of SO-coupling on BECs in radially periodic potential. Kartashov et al. studied two-component SO-coupled BECs in radially periodic potential and found that the system supports stable multiring solitons.[44]An immediate question is that, whether the SO coupling induces unknown types of ground state phases in spin-1 BECs confined in a radially periodic potential.
In this work, we consider the SO-coupled spin-1 BECs confined in a radially periodic potential. We first demonstrate numerically that SO-coupled antiferromagnetic BECs confined in the radially periodic potential support a multiring petal phase. In this situation, we can observe polar-core vortex from phase profiles,which is manifested as circularly symmetric distribution.Meanwhile,the number of petal in the system can be controlled by changing the SO coupling strength.Next,we show that SO coupling can induce multiring soliton structure in ferromagnetic BECs in the presence of the radially periodic potential. It is confirmed especially that the wavefunction phase of the ring corresponding to uniform distribution satisfies the rotational symmetry, and the wave-function phase of the ring corresponding to partial splitting breaks the rotational symmetry. For the case of ferromagnetic BECs, it is also found that the SO coupling can control the winding numbers of wave-function corresponding to each component.Furthermore, we investigate the effect of spin-dependent interaction on the ground state. The results show that adjusting antiferromagnetic spin-dependent interaction can control symmetry of the petal structure,and increasing ferromagnetic spin-dependent interaction makes the condensation tend to the uniform distribution. Finally,we also discuss the ground state properties under different spin-independent interactions for a given spin-dependent interaction parameter.Our findings open new directions for the studies of topological defects in SOcoupled quantum systems confined in a radially periodic potential.
2. Model and basic equations
We consider the two-dimensional spin-1 BECs with a Rashba SO coupling in the radially periodic potential. The mean-field Hamiltonian of this system is written as[13,34,35]

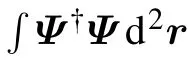


3. Results and discussion
3.1. SO-coupled antiferromagnetic BECs in the radially periodic potential
We first study the ground states of SO-coupled antiferromagnetic BECs in the radially periodic potential. To highlight the effect of the SO coupling,we fix the radially periodic potential and other parameters of the system. Figure 1 shows particle density profile and phase distribution of the ground states under different SO coupling strengths. For small κ,the condensation of the innermost ring is a uniform distribution.The condensation of outer ring exhibits the periodic density modulation along the azimuthal direction, which is a multiring petal phase as shown in Fig.1(a). As shown in density distributions of three components,the numbers of petals along the corresponding ring for each component are the same. In addition,the numbers of petals corresponding to the outer ring are more than those of the inner ring. From phase profiles we can observe polar-core vortex, which is manifested as circularly symmetric distribution. The structure of the polar-core vortex in terms of the individual spin components is as follows: a singly antivortex in the mF=+1 component,a singly vortex in the mF=?1 component,and no vortex in the mF=0 component.[7-12]When the SO coupling strength is further increased, the condensation of the innermost ring is split into petal structure. For the case of the outer ring, compared with the number of petal in Fig.1(a), it is found that the numbers of petals in Fig.1(b)significantly increase.

Fig.1. Ground states of the antiferromagnetic BECs for the different SO coupling strengths in the radially periodic potential. In this situation, the SO coupling can induce multiring petal phase. The first,second,and third columns indicate the particle number densities. The fourth,fifth,and sixth columns indicate phase distributions. (a)κ =0.4;(b)κ =1.2;(c)κ =1.6;(d)κ =2;(e)κ =4. The rest of parameters are λ0=3200,λ2=32,and V′=200.
For even larger values of SO coupling,such as κ=1.6,2,the ground state remains multiring petal structure. The petal structure corresponding to the innermost ring will change from hexagonal symmetry arrangement shown in Fig.1(c) to octagonal symmetry arrangement shown in Fig.1(d). From Fig.1(c)to Fig.1(d)we also observe that the number of petal along outer ring gradually increase through enhancing the SO coupling. Next, we consider very strong SO coupling case as shown in Fig.1(e), for example κ =4, the system always shows multiring petal phase, in which the number of petal reaches the maximum. Figure 1 confirms that the SO coupling can induce multiring petal phase in antiferromagnetic BECs in the presence of the radially periodic potential. As we all know that the SO coupling can induce stripe phase for the spinor BECs confined in harmonic trap.[30]In that situation the condensate density distributions show modified stripe with single direction. In the present work, because of the radially periodic potential the density distributions will show modified stripe along the ring direction. Therefore the ground state is called the multiring petal phase. Meanwhile,the numbers of petals in the system can be controlled by changing the SO coupling strength. It is worth noting that we can observe polar-core vortex with circularly symmetric distribution in phase profiles. These intriguing phenomena can be understood by the fact that the rotational symmetry is broken, and on the other hand,SO coupling greatly changes the motion of atoms and the azimuthal motion in the radially periodic potential. To get a deeper physical insight into multiring petal phase in antiferromagnetic BECs, we take petal numbers of the innermost ring as an example. In Fig.2, we plot the dependence of the petal numbers of the innermost ring on the SO coupling strength for fixed antiferromagnetic spin-dependent interaction. We find that the petal numbers can be controlled by adjusting the SO coupling strength. In addition, we also note that the petal numbers can display even or odd numbers.By comparing Figs. 2(a) and 2(c), the results show that the maximum number of petal becomes smaller when the antiferromagnetic spin-dependent interaction λ2is increased.

Fig.2. Petal numbers of the inner ring as a function of the SO coupling strength for the antiferromagnetic BECs. (a)λ2 =32; (b)λ2 =96; (c)λ2 =128;Here λ0=3200 and V′=200.
3.2. SO-coupled ferromagnetic BECs in radially periodic potential
We next consider the SO-coupled ferromagnetic BECs in the radially periodic potential. Figure 3 shows particle density profiles and phase distribution of ferromagnetic BECs under different SO coupling strengths. From density profiles we can see that the ground state displays multiring soliton phase for the ferromagnetic BECs, as shown in the first three columns of Fig.3. For small κ,it is found that there is phase separation between mF=+1 component and mF=?1 component, as shown in Fig.3(a). The low density for mF=+1 component is filled with mF=?1 component. When the SO coupling is enhanced, such as κ = 1.2, the density of the innermost ring is a uniform distribution, as shown in Fig.3(b). Meanwhile,the density of the outer ring is inhomogeneity distribution,which shows local splitting.For the case of phase profiles corresponding to the innermost ring,we can observe one-way circulating the wave-function phase with the rotational symmetry, which is similar to the plane wave.[30,40,43]More importantly, from the phase profiles of the innermost ring, one can see that there exists a winding number difference of one unit among different components,[41,43]which is highlighted by the black circle shown in Fig.3(b). From the phase profiles of the outer ring, one can see that there exists circulating the wave-function phase with the rotational symmetry broken.
For even larger values of SO coupling,such as κ=1.6,2,and 4, the ground state always shows multiring soliton structure. It is worth noting that the condensation of the innermost ring presents a periodic splitting through increasing the strength of SO coupling, as shown in Figs.3(c)-3(e), respectively. In addition, from the phase profiles of these ground states, one can see that the winding numbers of each component gradually increase with the increase of the SO coupling strength. Figure 3 confirms that the SO coupling can induce multiring soliton structure in ferromagnetic BECs in the presence of radially periodic potential. Meanwhile,increasing the strength of SO coupling can induce a periodic transition of the innermost ring from uniform distribution to partial splitting.Interestingly, it is also found that the wave-function phase of the ring corresponding to uniform distribution satisfies the rotational symmetry, and the wave-function phase of the ring corresponding to partial splitting breaks the rotational symmetry. In addition,we also demonstrate that the SO coupling can control the winding numbers of wave-function corresponding to each component. In order to see the multiring soliton structure more clearly,based on Figs.3(b),3(d),and 3(e),we plot the corresponding total particle number densities as shown in Fig.4, which clearly shows the multiring soliton structure.From Fig.3 we observe that the condensation density shows local splitting,which is caused by the phase separation among spin components.

Fig.3. Ground states of the ferromagnetic BECs for the different SO coupling strengths in the radially periodic potential. In this situation,the SO coupling can induce multiring soliton structure. The first, second, and third columns show the particle number densities. The fourth, fifth, and sixth columns show phase distributions. (a)κ =0.4;(b)κ =1.2;(c)κ =1.6;(d)κ =2;(e)κ =4. The rest of parameters are λ0=3200,λ2=?32,and V′=200.

Fig.4. Total particle number densities corresponding to the multiring soliton structure. (a)Total particle number densities corresponding to Fig.3(b). (b)Total particle number densities corresponding to Fig.3(d). (c)Total particle number densities corresponding to Fig.3(e).
3.3. Effects of spin-independent and spin-dependent interactions on ground states
Now we turn to effects of spin-independent and spindependent interactions on the ground states. Figure 5 shows particle density profiles and phase distribution of the ground states under different antiferromagnetic spin-dependent interactions for a given spin-independent interaction parameter.When antiferromagnetic spin-dependent interaction λ2=12,the ground state displays multiring petal phase as shown in Fig.5(a). At the same time, the petal structure corresponding to the innermost ring displays quadrangular symmetry arrangement. We also find the phase separation that is reflected in the densities of the mF=0 component and mF=±1 component. When the spin-dependent interaction is further increased,for example λ2=64,128,corresponding to Figs.5(b)and 5(c),respectively,the numerical results show that adjusting antiferromagnetic spin-dependent interaction can control symmetry of the petal structure and the number of petal in every ring.
Figure 6 shows particle density profiles and phase distribution of the ground states under different ferromagnetic spin-dependent interactions for a given spin-independent interaction parameter. When ferromagnetic spin-dependent interaction λ2=?12, the ground state displays multiring soliton phase as shown in Fig.6(a). From density profiles we also observe the phase separation between mF=1 component and mF=?1 component. With the increase of spin-dependent interaction, for example λ2=?64, ?128, the condensation of the innermost ring displays uniform distribution as shown in Figs.6(b)and 6(c).For the case of outer ring,the condensation tends to the uniform distribution compared with Fig.6(a).Figure 6 confirms that increasing ferromagnetic spin-dependent interaction leads to the uniform distribution of the condensation in the innermost ring. In addition, the condensation corresponding to the outer ring also tends to the uniform distribution.

Fig.5. Ground states under different antiferromagnetic spin-dependent interactions for a given spin-independent interaction parameter. (a) λ2 =12; (b)λ2=64;(c)λ2=128. The rest of parameters are λ0=3200,κ =1.2,and V′=200.
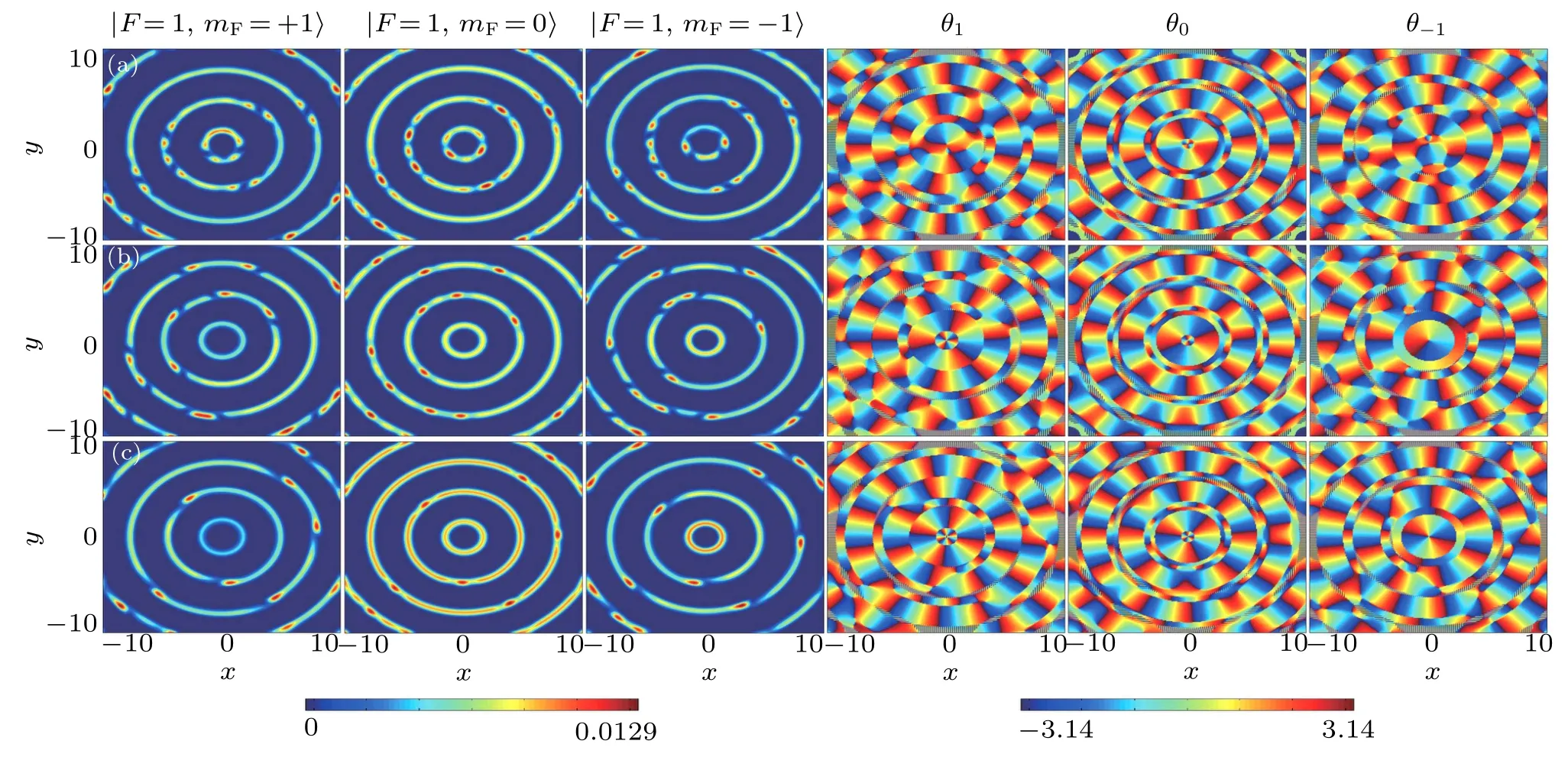
Fig.6. Ground states under different ferromagnetic spin-dependent interactions for a given spin-independent interaction parameter. (a) λ2 =?12; (b)λ2=?64;(c)λ2=?128. The rest of parameters are λ0=3200,κ =1.2,and V′=200.
In Fig.7, we discuss the ground state properties under different spin-independent interactions for a given spindependent interaction parameter. For a given antiferromagnetic spin-dependent interaction parameter, such as λ2=32,the results show that the ground states always show the multiring petal phase with symmetry arrangement as the spinindependent interaction is enhanced.The numbers of petals on each ring are almost unchanged. Increasing spin-independent interaction can induce the increase of the number of particles in the system,which only leads to the increase of the distribution area corresponding to the petal as shown in Fig.7(a1)and Fig.7(a2). For a given ferromagnetic spin-dependent interaction parameter, such as λ2=?32, the results show that the ground states always show the multiring soliton phase as the spin-independent interaction is enhanced. It is easy to see that the condensation of the innermost ring shows inhomogeneity distribution for very strong spin-independent interaction as shown in Fig.7(b2). In fact, the interactions can cause the variation of the local magnetic order,[5,34]leading to the interesting phenomenon shown in Figs. 5-7. Finally, we plot the dependence of the chemical potential on the strength of the SO coupling for the antiferromagnetic and ferromagnetic BECs as shown in Fig.8. It can be seen that the chemical potential is increasing with the SO coupling. From Fig.8(a)we find that the multiring petal phase in Fig.1(a) is smoothly changed to the phase in Fig.1(e) as κ is increased. The multiring soliton phase corresponding to Fig.3 is highlighted by the black arrow in Fig.8(b).

Fig.7. Ground states properties under different spin-independent interactions for a given spin-dependent interaction parameter. (a1)λ2 =32, λ0 =1200;(a2)λ2=32,λ0=6400;(b1)λ2=?32,λ0=1200;(b2)λ2=?32,λ0=6400. The rest of parameters are κ =1.2 and V′=200.

Fig.8. (a)Chemical potentialμ as a function of the SO coupling strength κ for the antiferromagnetic BECs. The multiring petal phase Fig.1(a)is smoothly changed to the phase Fig.1(e)as κ is increased. Here λ0=3200 and λ2=32. (b)Chemical potentialμ as a function of the SO couplig strength κ for the ferromagnetic BECs. The multiring soliton phase corresponding to Fig.3 is highlighted by the black arrow. Here λ0=3200 and λ2=?32.
4. Conclusion
In conclusion, we have investigated the ground states of SO-coupled BECs confined in the radially periodic potential.For the antiferromagnetic BECs, we have demonstrated that the SO coupling can induce the multiring petal phase. The polar-core vortex was found in phase profiles,which is manifested as circularly symmetric distribution. For the ferromagnetic BECs, it was found that the SO coupling can induce multiring soliton structure. Especially, it was confirmed that the wave-function phase of the ring corresponding to uniform distribution satisfies the rotational symmetry, and the wavefunction phase of the ring corresponding to partial splitting breaks the rotational symmetry. We have shown that adjusting the SO coupling strength can control the number of petal in antiferromagnetic BECs and the winding numbers of wavefunction in ferromagnetic BECs. The influences of the interactions on the properties of the ground states have also been investigated. This work provides the basis for further investigations of the quantum system with the high-dimensional SO coupling[46]in the presence of the radially periodic potential.
- Chinese Physics B的其它文章
- Transport property of inhomogeneous strained graphene?
- Beam steering characteristics in high-power quantum-cascade lasers emitting at ~4.6μm?
- Multi-scale molecular dynamics simulations and applications on mechanosensitive proteins of integrins?
- Enhanced spin-orbit torque efficiency in Pt100?xNix alloy based magnetic bilayer?
- Soliton interactions and asymptotic state analysis in a discrete nonlocal nonlinear self-dual network equation of reverse-space type?
- Discontinuous event-trigger scheme for global stabilization of state-dependent switching neural networks with communication delay?

