Breather solutions of modified Benjamin–Bona–Mahony equation
G T Adamashvili
Technical University of Georgia,Kostava Street 77,Tbilisi,0179,Georgia
Keywords: modified Benjamin–Bona–Mahony equation, generalized perturbation reduction method, vector breather,nonlinear waves
1. Introduction
A solitary wave is a localized highly stable nonlinear wave that maintains its profile when it propagates at a constant speed through a medium.The existence of solitary waves in the form of a soliton and its various modifications, including breather (pulsing soliton) and vector soliton, among others, is one of the most striking demonstrations of the nonlinear properties of the medium in which they are propagating.Such waves are encountered in a wide variety of research fields pertaining to optics,acoustics,plasma,hydrodynamics,particle physics, etc. Depending on the nature of the nonlinearity,various mechanisms of the formation of nonlinear solitary waves are realized. However,the general properties of solitary waves in different materials and physical situations can be similar. Usually,two main types of solitary waves are considered:single-component (scalar) and two-component (vector) nonlinear waves. Among single-component solitary waves, soliton and breather are investigated quite often. However, the breather is of special interest because it can be propagated at a relatively low intensity of the wave in comparison to the soliton. They have been studied for a very long time, both theoretically and experimentally, in a lot of nonlinear physical phenomena.[1–23]In addition to single-component scalar breathers, two-component waves, such as vector solitons, are also considered in various physical systems, such as optical waveguides.[24,25]Recently,in optics, as well as in acoustics,some special varieties of two-component waves, which are the bound state of two small-amplitude scalar one-component breathers with the same polarization, have been investigated.One breather oscillates with the sum, and the other with the difference of the frequencies and wavenumbers(SDFW).This nonlinear two-component wave has a very special profile that differs in shape among all other nonlinear solitary waves(see Fig.1). In the theory of self-induced transparency,such a nonlinear solitary wave is called the vector 0π pulse.[26–30]
The behavior of the single-component and twocomponent solitary waves can be described mathematically by means of nonlinear partial differential equations. These include the Sine–Gordon equation (SGE), the Maxwell–Bloch equations, the Maxwell–Liouville equations, the wave equation in Kerr media, the system of wave equation and material equations for two-photon resonant transitions,the system of the magnetic Bloch equations and the elastic wave equation, among others. The inverse scattering transform (IST),the perturbative reduction method (PRM), and several other approaches to solve the nonlinear differential equations and to analyze the solitary waves have been applied.[1,31–36]In particular, a small-amplitude breather solution of SGE can be obtained by means of IST (see Appendix A: As a point of clarification, there have been two different definitions of“breathers” which do cause confusion. The standard definition of“breathers”was a bound state of a two-soliton solution of the nonlinear wave equation, for instance, SGE, Bloch–Maxwell equations, etc. and is manifestly stable against infinitesimal perturbations of the initial data. But certain twosoliton solutions of some other nonlinear equations, such as the scalar NSE and others, have also been called “breathers”solutions, provided that each soliton in the breather had exactly the same velocity, such that they would travel as a unit and would oscillate. But they were manifestly unstable to almost any infinitesimal perturbation of the initial data, upon which they would slowly separate, since the binding energy was zero. We are considering the original definition of the breather,as being a stable,bound state of two solitons. In the low intensity limit, the envelope of this breather is described by a one-soliton solution of the scalar NSE. Such situation take place, for instance, for SGE and Bloch–Maxwell equations when small amplitude breathers of these equations are connected with the one-soliton solution of the scalar NSE[1,6]).
The two-component vector breathers oscillating with the SDFW have been considered for optical and acoustic waves by means of the Maxwell–Bloch equations, the Maxwell–Liouville equations, and SGE, among others, using the recently developed generalized version of the PRM.[26–30,38,39]But a question is evoked: Is this two-component nonlinear wave specifically for optics and acoustics, or does it have a more general character, and can it be met in other fields of research, such as plasma, hydrodynamics, etc.? Regarding this, it is natural to consider other materials and corresponding nonlinear differential equations. Physical systems, other than those in optics and acoustics,can be described by means of the nonlinear dispersive modified Benjamin–Bona–Mahony(MBBM)equation. This equation was derived to describe an approximation for surface long waves in dispersive nonlinear materials,with phonon properties in the anharmonic crystal lattice, acoustic-gravity waves in compressible fluids, and hydro-magnetic waves in cold plasma.
The generalized MBBM equation has the form[40–45]

When n = 2 this equation called the nonlinear dispersive MBBM equation

or in the dimensionless form[44]

where u(z,t) is a real function of space and time, z is spatial variable and t is time variable. C, β, and a are arbitrary constants.
Equation (1) have been considered as an improvement of the modified Korteweg–de Vries (MKdV) equation which is also well known in different field of research and applications.[41,43–46]
Sometimes,another form of the MBBM equation is also considered[47,48]

The linear part of MBBM equation(1)is given by

which describes dispersive effect to the equation and yields dispersion relation between the wavenumber k and frequency ω:

In the system of coordinates moving along the axis z with velocity C,equation(1)is transformed to the MKdV equation

where

Equation (3) has been proposed as a model to describe the nonlinear evolution of plasma waves, the dynamics of thin elastic rods,phonons in anharmonic lattices,meandering ocean currents, traffic congestion, hyperbolic surfaces, ionacoustic solitons,Alfven waves in collisionless plasmas,slagmetallic bath interfaces, and Schottky barrier transmission lines, among others.[49]There are many different approaches in finding the solutions of the MKdV equation; in particular, through the means of the IST and the single-component(scalar) N-solitons and breathers, exact solutions have been studied.[49,50]
Although the properties of various solitary waves of the MBBM (MKdV) equation have been studied, a twocomponent breather oscillating with the SDFW, which is the superposition of two single-component breathers,has not been considered till date. The purpose of the present work is to theoretically investigate the connection between the MBBM equation(1)and the coupled nonlinear Schr¨odinger equations(NSEs)and to study the two-component breather solution oscillating with the SDFW of the MBBM equation by using the generalized PRM and the comparison with the singlecomponent (scalar) breather of this equation analyzed by the PRM.
The rest of this paper is organized as follows: Section 2 is devoted to the two-component (vector) breather solution oscillating with the SDFW of the MBBM equation by using the generalized version of the PRM.In Section 3,we will investigate the one-component (scalar) breather solution of the MBBM equation with the PRM in standard form. Finally, in Section 4,we will compare the two methods,PRM in standard form and the generalized PRM and corresponding solutions,and discuss the obtained results.
2. Vector breather and the generalized PRM
In the beginning,we simplify Eq.(1)by using the method of slowly varying envelope approximation in the following form:[43,51]






and the connection between the parameters ω and k, is given by Eq.(2).


where ε is a small parameter,


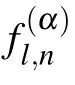

Substituting Eq.(8)into Eq.(7),we obtain

where

There are four independent equations for the different values l=±1 and n=±1.
Equating to zero, the terms with the same powers of a small parameter ε,we obtain a series of equations. In the first order of ε,we obtain the following equation

From Eqs. (10) and (11), we can establish a connection between different values of the parameters ?l,nand Ql,n. In particular,when


From Eq.(9),in the second order of ε,we obtain the following equation:

Taking into account Eqs.(12)and(13),from Eq.(14)we obtain the following equations:

From Eq.(9), we have in the third order of ε the system of equations proportional to Z+1and Z?1,respectively


We consider the equation proportional to the Z+1in detail, the complex-conjugation equations proportional to the Z?1can be considered similarly.
After a transformation back to the variables z and t,from Eq.(16)we obtain the coupled NSEs in the following form:
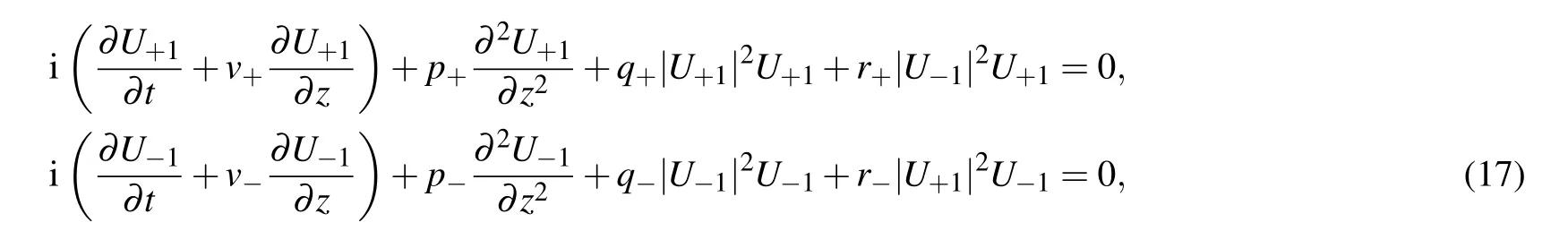
where
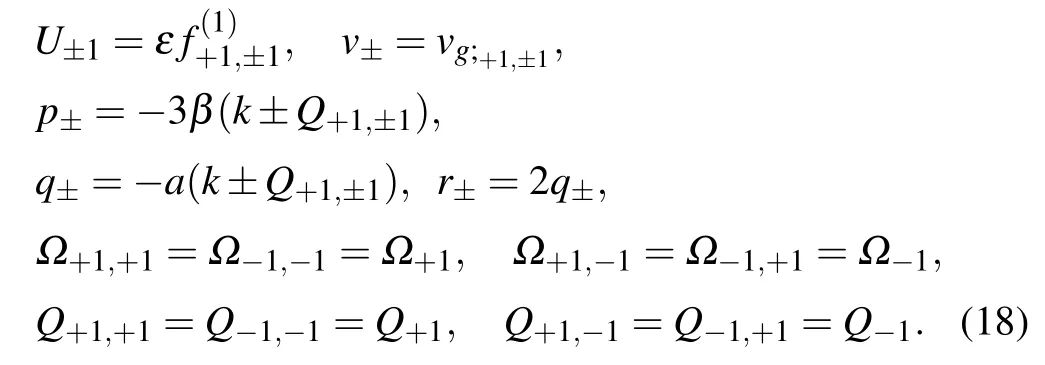
Equations (17) are the characterizing bound state of the two breathers. One breather is described by means of the function U+1and the second breather by the function U?1.These breathers propagate in the same direction,with the same constant velocities, and have identical polarizations. In the process of propagation, they interact with each other and exchange energy. This connection between breathers is characterized by the cross terms in Eqs. (17), r+|U?1|2U+1, and r?|U+1|2U?1. As a result, we obtain one steady-state twocomponent vector pulse that consists of the two breathers.In order to describe properties of the vector two-component pulse, we have to find solutions for the coupled NSEs for the auxiliary functions U+1and U?1.
We will seek the steady-state solutions of Eqs. (17) for the functions U±1in the following form:

where ?±=k±z?ω±t are the phase functions for each components, K±,k±, and ω±are constants. The standard way to ensure the stationary character of the envelope function S(ξ)entails depending on space coordinate and time only through the variable ξ =t ?(z/V0), where V0is the nonlinear twocomponent pulse velocity. We consider that valid following inequalities:

Substituting Eqs. (19) into Eqs. (17), we obtain the explicit form of the envelope function and connections between different parameters of the breathers


Substituting Eqs.(19)and(21)into Eqs.(8)and(5), we obtain the two-component vector breather oscillating with the SDFW of the MBBM equation(1)in the following form:

where T is the width of the two-component nonlinear pulse

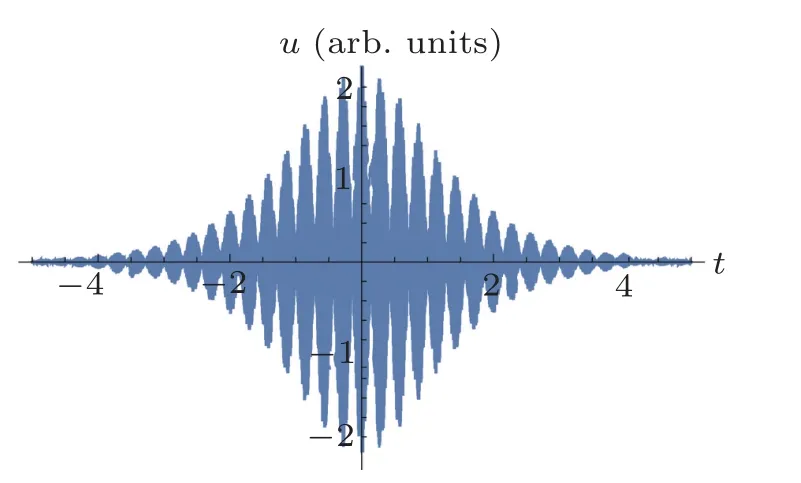
Fig.1. Plot of the two-component breather oscillating with the SDFW of the MBBM equation(22)at a fixed value of the z coordinate.
Equation (22) describes the nonlinear two-component vector pulse (vector breather) that consists of the two breathers. One of them oscillates with the sum of the frequencies ω+?+1and wavenumbers k+Q+1(to take into account Eqs.(20))and the other with the difference of the frequencies ω ???1and wavenumbers k ?Q?1. The parameters of the nonlinear wave by Eqs. (15), (18), (21), and (23) are determined. The corresponding plot of the two-component vector breather oscillating with the SDFW of the MBBM equation at a fixed value of the z coordinate for the values of the parameters ω/?±1=103,?+1/??1=0.83 is presented in Fig.1.
3. One-component breather
In the present section, we will consider the onecomponent breather solution of the MBBM equation (1) by the PRM.The function u is expanded in a power series of ε as follows:[36]

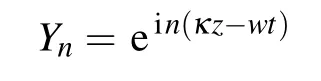
is the rapidly varying part,while the slow variables
ζ =εκ(z?vgt), τ =ε2t, vg= dw/dκ.
We assume that they satisfy the inequalities


Substituting the expansion(24)into Eq.(1),we obtain the equation

To determine the functions of f(α)n,we equate to zero the different terms corresponding to the same powers of ε.
In the first order in ε,we obtain the following equation
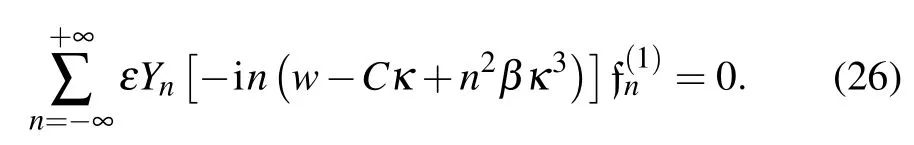
From Eq.(26),we obtain the dispersion relation


In the second order in ε,we obtain the following equation



Using the expressions

we can transform the equations(29)to the form


where
If we make the transformation of the variables Eq. (4),from Eq.(30),we will finally obtain the NSE in the form

where

Equation(31)has the soliton solution[21–24]

where

K is the amplitude of the NSE soliton,Vbis the velocity of the nonlinear wave,λlis the envelope of the soliton.
Substituting the soliton solution for λlfrom Eq. (33) in Eq.(24),we obtain for the envelope for u the one-component(scalar) breather solution of the MBBM equation (1) in the form

From Eq. (35), it is obvious that the trigonometric function points to the existence of oscillation, and this leads to the conclusion that the soliton solution of the NSE (33)for the auxiliary function λlis transformed to the onecomponent breather solution(35)of the MBBM equation for the function u(z,t). The profile and parameters of the onecomponent breather of the MBBM equation are determined from Eqs. (32), (34), and (35). The connection between parameters w and κ is determined from Eq. (27). The corresponding plot of the one-component scalar breather of the MBBM equation at a fixed value of the z coordinate for the values of the parameter w=50(at the same width as the vector breather in Fig.1)is presented in Fig.2.

Fig.2. Plot of the one-component breather of the MBBM equation(35)at a fixed value of the z coordinate.
From Eqs. (35) and (A2), it is evident that the onecomponent breather solution of MBBM equation coincides with the small-amplitude breather of SGE with precision to the notation(see Appendix A).
4. Conclusion
We consider the formation of nonlinear waves in various physical systems (anharmonic crystals, hydrodynamics,plasma, etc.) that are described by the MBBM equation (1).Using a recently developed mathematical approach, the generalized PRM,it became possible to obtain a new solution of the MBBM equation,which is a nonlinear combination of the components of two breathers. One component oscillates with the sum,and the second with the difference of the frequencies and wavenumbers. Both components have the same polarization, and as a result of the superposition of their amplitudes,a nonlinear pulse with a specific profile is obtained. Although the analytical expression of the pulse Eq.(22)differs from the analytical expression of the vector 0π pulse of the self-induced transparency studied at the beginning in nonlinear optics,and later in nonlinear acoustics, the corresponding graphical expressions are similar(see Fig.1).[26–30]
We also obtained a one-component breather solution of the MBBM equation by means of PMR in a standard form. This wave completely coincides with the low-amplitude breather solution of SGE.On comparing the analytical expressions and corresponding profiles of the two-component (vector)and one-component(scalar)breathers of the MBBM equation,it becomes obvious that they are completely different.Indeed, the vector breather is the bound state of the two scalar breathers when one breather oscillates with the sum and the other with the difference of the frequencies and wavenumbers. The difference between the two-component and onecomponent waves is especially evident when comparing the corresponding profiles in Figs. 1 and 2. A scalar breather is characterized by one amplitude K and two oscillating parameters w and κ. The relationship between them is illustrated through Eq. (27) and the parameters are determined from Eq.(34).
On the other hand,a vector breather is characterized by a larger number of parameters: two amplitudes K+and K?,and four oscillating parameters ?+1,??1,Q+1,and Q?1. The relationship between these oscillating parameters is determined by Eqs. (12) and (13), while the relationship between the remaining parameters is determined by Eqs.(21)and(23).
The study of the two-component breather solutions became possible due to the generalized PRM,which allowed us to expand the number of auxiliary functions and parameters compared to the standard PRM. In particular, in the generalized PRM,we used two complex functions, f±1,±1and f±1,?1,and eight parameters, ?l,nand Ql,n; however, in the standard PMR, there is only one complex function, fn, and two parameters, w and κ, which are not enough to describe twocomponent waves.
The results obtained above allow us to reach an important conclusion, which is that the generalized PRM allows us to obtain a new solution Eq. (22) (see Fig.1) of the MBBM equation (1). Such a nonlinear two-component pulse, previously studied in optics and acoustics, can also be formed in other physical systems, in particular, in anharmonic crystals,hydrodynamics, plasma, etc. The present work significantly extends the class of materials and physical situations in which vector breathers oscillating with the SDFW can be formed.Consequently, the existence of the vector breathers oscillating with the SDFW has a general character and can be met in completely different physical systems and various physical situations.
Appendix A
The breather solution of SGE,which is stable solution to relatively infinitesimal perturbations of the initial data,can be obtained by the IST and written as[31–34]

where A is the amplitude of the wave, the functions ?1and ?1are determined in Ref.[31]. When A ?1, the breather in Eq.(A1)can be reduced to a small amplitude breather

- Chinese Physics B的其它文章
- Novel traveling wave solutions and stability analysis of perturbed Kaup–Newell Schr¨odinger dynamical model and its applications?
- A local refinement purely meshless scheme for time fractional nonlinear Schr¨odinger equation in irregular geometry region?
- Coherent-driving-assisted quantum speedup in Markovian channels?
- Quantifying entanglement in terms of an operational way?
- Tunable ponderomotive squeezing in an optomechanical system with two coupled resonators?
- State transfer on two-fold Cayley trees via quantum walks?

