The Mordell-Weil Groups of Cubic Pencils

Mo Jiali

(Department of Mathematics,Soochow University,Suzhou 215006,China)

Abstract In this paper we study the influences of the base points of cubic pencils on the Mordell-Weil groups.Specifically,we investigate and classify the cubic pencils with 8,7 and 6 base points in general position,and give some applications.

Key words Base point Cubic pencil Elliptic curve Mordell-Weil group

1 Introduction

The elliptic curve is one of the most classical,fundamental and fascinating objects in mathematics.The cubic pencil is an useful method for studying elliptic curves.

LetH1,H2∈k[X,Y,Z](kis an algebraically closed field of characteristic zero)be two homogenous cubic polynomials without common factor.Consider the cubic pencil

If it contains at least one singular cubic curve,then it defines a genus one fibration over P1with homogeneous coordinates [s,t](possibly as a projective surface in P2×P1after resolving singularities ofSs,t).Sincekis algebraically closed,Ss,tgives an elliptic surface with sections given by the base points of the cubic pencil.It is well known that each cubic pencil in P2is a rational elliptic surface by blowing-up of nine(including infinitely near)base points.Moreover,we have the following theorem([1],Theorem 5.6.1):Over an algebraically closed field,every rational elliptic surface(with section)admits a model as a cubic pencil.

In this paper,we assume thatSis a smooth projective surface having a relatively minimal elliptic fibrationf:S→Cwith the zero section(O)over a curveC.LetEbe the generic fiber offwhich is an elliptic curve over the function fieldK=k(C).Assume thatfhas at least one singular fiber.Then the groupE(K)ofK-rational points is finitely generated(Mordell-Weil theorem,see[2]).It can be identified with the group of sections off.In[3],Manin and Shafarevich computed the Mordell-Weil group of the fibration corresponding to a general cubic pencil in P2.They proved that the Mordell-Weil group of above fibration isE8.

If we denote bySthe blow-up of P2at the nine base points,the pencil defines an elliptic fibrationf:S→P1such that the nine exceptional curves arising from the blow-up give nine sectionsP0,···,P8off.ChooseP0as the zero section(O),and letEbe the generic fibre off.ThenP1,···,P8generate a subgroup of index 3 inE(K),and there is a unique pointQ∈E(K)such that=3Q.Together withP1,···,P7,the pointQgenerates the full Mordell-Weil groupE(K).

The above result is quite striking since it concerns a general rational elliptic surface(with section):all cubic pencils with Mordell-Weil rank less than 8 lie on a hypersurface inside the moduli space of cubic pencils(the discriminant divisor).It might therefore come as a little surprise that the general case seems to be exceptional within rational elliptic surfaces.Indeed,papers[4,5,6]show that for any cubic pencil of Mordell-Weil rank 4 to 7,the base points generate the full Mordell-Weil group.At the other end of the scale,[7,8]solved the case of Mordell-Weil rank zero where there is also a model as a cubic pencil whose base points generate the finite Mordell-Weil group.

Moreover,in[9],Ogusio and Shioda classified the Mordell-Weil groups of a rational elliptic surface.In[10],[11]and[12],the authors also computed the Mordell-Weil groups of the fibrations corresponding to the curve pencils of high degree in P2.

It is well known that 9 points in general position determine a unique cubic curve in P2.In this paper,we will give more accurate results on the Mordell-Weil groups of fibrations corresponding to the cubic pencils with 8,7 and 6 base points in general position(npoints in general position means that there is no 3 points on a line and no 6 points on a conic).For the Mordell-Weil groups of such pencils,we have the following theorem.

Theorem 1.1Givenn(=8,7,6)points in general position in P2.Then in the following cases:

(1)8 points are simple base points of a cubic pencil(1.1)(in fact there are 9 simple base points),

(2)7 points are only simple base points of a cubic pencil(1.1),and every element of the above cubic pencil is irreducible,and

(3)6 points are only simple base points of a cubic pencil(1.1),and every element of the above cubic pencil is irreducible,the Mordell-Weil groups of fibrations related to the corresponding cubic pencils areE8,,respectively.

Remark 1.1The condition of“in general position”is essential.

Example 1.1In[7],Beauville gave a cubic pencil(elliptic surface)

whereH1=(X+Y)(Y+Z)(Z+X),H2=XY Z.In this case,there are 8 base points not in general position(it has 3 base points on a line),and rank(E(K))=0.

Moreover,we have the converse form of Theorem 1.1:

Theorem 1.2Letf:S→C=P1be an elliptic fibration with the zero section (O).If the Mordell-Weil groups,thenfcan be obtained by blowing-up the cubic pencils with exactly 9,7,6 simple base points,respectively.

Remark 1.2In fact,Theorem 1.2 is implied in[13]in an unobvious form.In this paper,we provide a new proof for it.

The cubic pencils of the above Theorem 1.1 can be classified as follows:

Theorem 1.3Each of the fibrations with Mordell-Weil groupsE8,corresponding respectively to the cubic pencils (1)-(3) in Theorem 1.1 is isomorphic to one of the following two types of fibrations with respect to each Mordell-Weil group:

A Del Pezzo surfaceXis either P1×P1or the blow-up of P2inm(m=1,···,8)points in general position.The degreedofXis defined asd=9-m(see[14]).As an application,we give a new proof to the numbers of(-1)-curves in Del Pezzo surfaces(see[15]).

Theorem 1.4There are 240,56,27 (-1)-curves in the Del Pezzo surface of degree 1,2,3,respectively.

The paper is organized as follows.In Section 2,we recall some related definitions and notations.Then,in Section 3,4 and 5,we prove Theorem 1.1,1.2 and 1.3,respectively.Finally,in Section 6,we give some applications.

2 Definitions and notations

In this section,we recall some related definitions and notations.

Definition 2.1A base point in a cubic pencil is simple if it is a normal crossing point of two general elements in the cubic pencil.

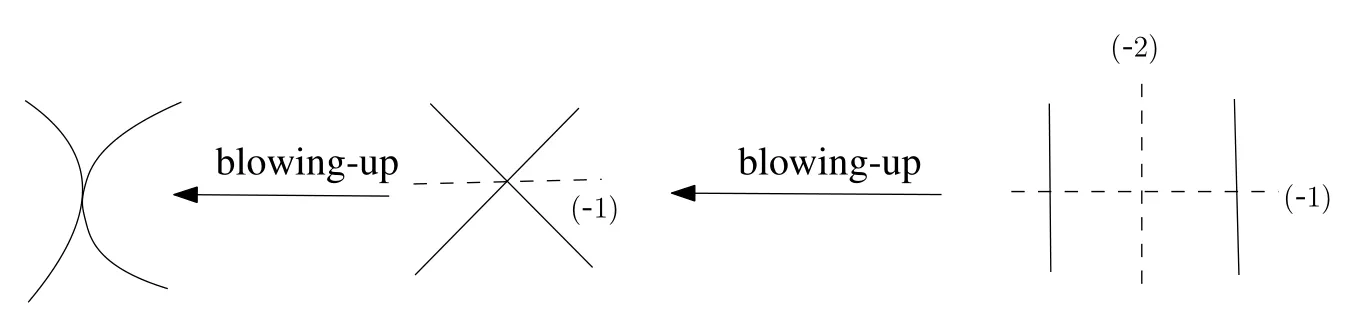
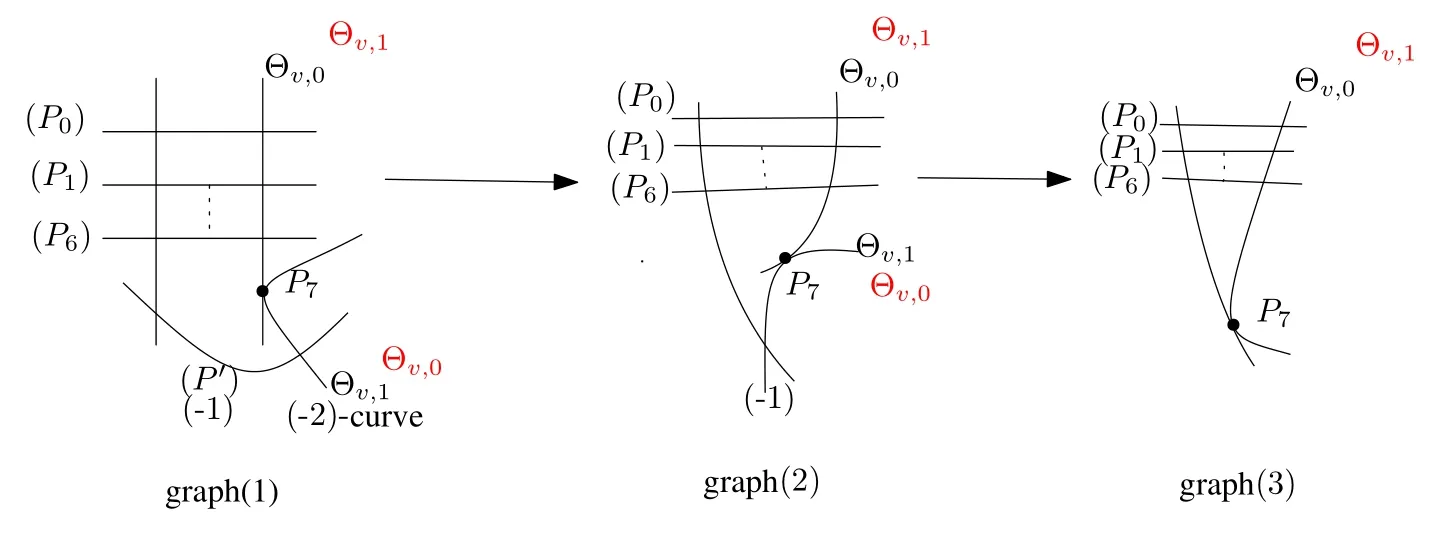
Definition 2.2A latticeLof rankris a root lattice of typeEr,if there exists a basis{α1,α2,···,αr}ofLsuch that for 1≤i =0 unless(Er):<αi,αj >=-1 fori+1=j

In this paper,we are especially concerned withE6,E7andE8.For instance,we choose a basis{α1,α2,···,α6}ofE6such that<αi,αi >=2(i=1,2,···,6)and<αi,αj >=-1 fori+1=j <6,ori=3,j=6(see Figure 1).

Definition 2.3The dual latticeL∨of an integral latticeLis defined by

with pairing naturally extended fromLtoL ?Q.

As the name suggests,the dual lattice can also be defined as a natural lattice structure on the dual moduleL∨=Hom(L,Z).Though this viewpoint is useful in many contexts,we will always regardL∨as a lattice containingLas a sublattice of finite index.

Now,we recall and fix some standard notations in dealing with Mordell-Weil lattices(cf.[16]).The readers can refer to[2,9,17]for more details.

?k:an algebraically closed field of characteristic zero.

?K=k(C):the function field ofCoverk.

?E(K):the finitely generated Mordell-Weil group,i.e.,the group ofK-rational points of an elliptic curveEoverKwith the finitely generated zero section(O).

?:the height pairing (P,Q∈E(K)),as defined by Shioda.It is a symmetric bilinear pairing and a positive-definite modulo torsion.

?f:S→C=P1:the associated elliptic surface(the Kodaira-Neron model)ofE/Kwith at least one singular fiber.AK-rational pointP∈E(K)is identified with a section off.

? (P):the curve onSdetermined by a sectionP,esp.(O)is the zero section viewed as a curve onS.

? (P,O):the intersection number of(P)and(O).

?χ(S):the arithmetic genus ofS(a positive integer).

?R:={v∈C|f-1(v)is reducible}.

?mv:the number of components of fiberFvof an elliptic surface.

? Θv,i(0≤i ≤mv-1):irreducible components off-1(v)(v∈R),withi=0 corresponding to the identity component,which intersects with the zero section(O).

?Tv:the lattice generated by Θv,j(j >0) with the sign changed.There are root lattices of typeA,D,Edetermined by the type of reducible fiberf-1(v).

?T=:the trivial lattice.

?E(K)0:the narrow Mordell-Weil lattices ofE/Kdefined as

It is a certain subgroup of finite index inE(K).

?ρ(S):the rank of the N?ron-Severi group.

?≡:numerical equivalence(in the case of elliptic surface,numerical equivalence is equivalent to algebraic equivalence).

?Ip(H1,H2):the intersection number ofH1andH2atp.

?lp(H1):the multiplicity of curveH1atp.Whenpis a singular point,lp(H1)≥2.

3 Proof of Theorem 1.1

In this section,we will prove Theorem 1.1.Let us firstly give several lemmas.

Lemma 3.1Given a rational elliptic surfacef:S→P1with zero section(O).LetEbe a generic fiber.IfCis a(-k)-curve(k≥2)overS,thenCis a component of singular fiber andk=2?IfCis a(-1)-curve,thenCis a section.

ProofSuppose thatCis not a component of singular fiberF.Then (C,F)>0.Since we haveχ(S)=1,we conclude fromKS≡(2g(P1)-2+χ(S))Fin [18] thatKS≡-F.It follows thatC2=-k,g(C)=0 and (KS,C)+C2=2g(C)-2=-2,and then (KS,C)≥0.This gives(KS,C)=-(F,C)≤0,which contradicts to our assumption.Hence(F,C)=0 and consequently,Cis a component of singular fiber.From(KS,C)=0 we can getC2=-k=-2.

IfCis a(-1)-curve,we can get(KS,C)=-1 andKS≡-Eby the above two formulas.Thus,(KS,C)=((-E),C)=-1,andCmust be a section.

The proof is complete.

Lemma 3.2LetH1andH2be two cubic curves.

(i)IfIp(H1,H2)=n(n=2,3),then there exists at least a smooth cubic in the cubic pencilsH1+tH2.

(ii)IfH1is smooth,then there exists a smooth cubicH3in the above cubic pencil,andH3H1.

Proof(i)Iflp(H1)=m(m≥2),lp(H2)=n(n≥2),thenIp(H1,H2)≥4.Hence,there exists at least a smooth cubic.

(ii)SupposeH1is smooth.IfH2is also smooth,then(ii)is true.IfH2is not a smooth cubic,then we takeH3=H1+H2as a new cubic,which is smooth.

The proof is complete.

In the following,we will prove Theorem 1.1.

Proof of Theorem 1.1(1)8 points are in general position.In this case,we consider firstly that this cubic pencil contains a reducible cubicC.ThenCmust be split into a conic and a line.On a conic,there are no more than 5 points in their general positions,and at least 3 points remain on a line(the base points may be the intersection of the line and the conic),which is a contradiction.So every cubic in this cubic pencil is irreducible.

Secondly,since every base point in the cubic pencil is simple,we get 9 simple base points.By blowing-up such 9 points,we can getf:S→P1with zero section(O)and 9(-1)-curves,which are all sections.Thus,every fiber is irreducible.

Thirdly,sinceSis a rational surface,ρ(S)=10,and all fibers are irreducible,we have rank(E(K))=8 by the formula rank(E(K))=ρ(S)-2-.From the Main Theorem in [9],we haveE(K)E8.

(2)7 points are in general position.In this case,every cubic in this cubic pencil is irreducible.As we have 7 base points in the cubic pencil which are simple base points,according to Lemma 3.2,2 smooth cubics can be constructed which are tangent atp.Then by blowing-up these 7 base points and the multiple base point,we obtainf:S→P1with zero section(O),8(-1)-curves and one(-2)-curve(see Figure 2).It is clear that the(-1)-curves must be sections.According to Lemma 3.1,the(-2)-curve must be a component of a singular fiber.Hence we just have one singular fiber with 2 components.Then,by the formulas rank(E(K))=ρ(S)-2-and=1,we have rank(E(K))=7.By the Main Theorem in[9],we haveE(K).

Figure 2 The blow-up of base points

(3)8 points are in general position.The proof is similar to Case(2).

The proof is complete.

4 Proof of Theorem 1.2

Proof(1)E(K)E8.Firstly,we construct 8(-1)-curves inE(K),which are disjoint to each other.SinceE(K)0E8,we only need to consider the above(-1)-curves inE(K)0.Let(P0)=O,(Pi)=,i=1,2,···,7(Cf.Definition 2.2 and Figure 3).Then=2 and=1(ij,1≤i,j≤7).By the formula in[18],=χ(S)+(Pi,O)+(Pj,O)-(Pi,Pj),=2χ(S)+2(Pi,O),which follows(Pi,Pj)=0 and(Pi,O)=0.

Then,we contract the 8 (-1)-curves (Pi)(i=0,1,2,···,7) to get a cubic pencilCtwith 8 base points.It is well known that every smooth elliptic curve can be isomorphically mapped to a smooth cubic in P2.Now,we choose two general curves inCt,and isomorphically map them into P2.By fixing 4 simple base points in P2,and letting the above 4 points become the images of the 4 base points ofCtin P2,we get a unique cubic pencil in P2.By the construction,we see that there must be 8 simple base points in the planar cubic pencil.Then by the Bezout theorem,the cubic pencil must have 9 simple base points.

(2)E(K).In this case,we need to construct 7 (-1)-curves inE(k)0which are disjoint to each other.Let(P0)=(O),(Pi)=,i=1,2,···,6.Similar to the proof of the caseE(K),we have(Pi,Pj)=0 and(Pi,O)=0.

Then,we construct another(-1)-curve(P′)such that

(i)(P′)is disjoint to Θv,0;

(ii)(P′,Pi)=0,i=0,1,2,···,6.

Denote the Gram matrix ofE7byG,and letβi,i=1,2,···,7,be the basis of.LetG′be the Gram matrix of.Then we have

Now takeP′=β6.Since

we have

Note thatG=GG-1GT,then(α1,α2,···,α7)T=G(β1,β2,···,β7)T.So we can useβ1,β2,···,β7to representα1,α2,···,α7,hence to representPi,i=0,1,2,···,6,and then get<β6,Pi >=1.Since<β6,Pi >=χ(S)+(β6,O)+(Pi,O)-(β6,Pi)-,and=0,we get(β6,Pi)=0(i=1,2,···,6).

Figure 3 The process of contracting(-1)-curves

SinceE(K),T=A1,the singular fiber isIII(orI2).The process of contracting(-1)-curves is as follows:Firstly,we start to blow down(P′)and get graph(2)in Figure 3.Then by blowing down Θv,1we get graph(3)in Figure 3.Finally we blow down(Pi),i=0,···,6 in turn and get a cubic pencilCtwith 7 simple base points.Then we can also isomorphically map them into P2and fix 4 simple base points in P2,and get a unique cubic pencil in P2.The analysis here is similar to the proof for the caseE(K).

(3)E(K).The proof for this case is similar to the caseE(K).

The proof is complete.

5 Proof of Theorem 1.3

Lemma 5.1Letf:S→P1be a fibration with the zero section(O),andEbe a generic fiber.Iffhas no singular fibers,thenScan’t be a rational surface.

ProofAssumef:S→P1is a fibration with no singular fibers.Because there is no Kodaira fibration over P1,thenfmust be a trivial fibration,thusS=E×P1is not a rational surface.

The proof is complete.

Lemma 5.2IfH1andH2are two cubic curves in P2,andIp(H1,H2)≥2.Then there exists a cubic,which is singular atpin the cubic pencilsH1+tH2.

ProofIfH1orH2is singular atp,then the conclusion is obviously true.Now assumeH1andH2are smooth atp.SinceIp(H1,H2)≥2,H1andH2have the same tangent atp.Then we can choose a numberkto make the coefficient of the lower degree term(degree ≤1)ofkH1-H2to be 0.Hence,there exists a cubic singular atpin the cubic pencilsH1+tH2.

The proof is complete.

Now we are ready to prove Theorem 1.3.

Proof of Theorem 1.3Firstly,when the Mordell-Weil group of fibrations related to the corresponding cubic pencil isE8,we know that every element in the cubic pencil is irreducible by Theorem 1.1.From Lemma 5.1,we see there is a singular element in the cubic pencilsH1+tH2.Because every cubic is irreducible,then the singular cubic is either a cusp curve or a node curve.In the former case,letH0be the cusp curve and take it as the formy2=x3after some suitable coordinate transforms.LetH3be another smooth curve,then{sH1+tH2}={sH0+tH3}andH0∩H2={p1,p2,···,p9}.From the Cayley-Bacharach theorem,p9can be determined byp1,p2,···,p8,and further more,eachpican be represented byvionH0:pi=,i=1,2,···,8.

After blowing-up all the above base points,everypicorresponds to a sectionPiinE(K).AssumeP9=O.Letui=1/vi,thenuicorresponds to sectionPi,i=1,2,···,8.Each integral sectionPcorresponds to a pointpinH0.BecauseE(K)E8,and rank{P1,···,P8}=8,Pis the unique Q coefficient combination ofPi.Moreover,pis the unique Q coefficient combination of{u1,···,u8}by the additive law ofH0.Then,every integral sectionPcorresponds to the unique Q coefficient combination of{u1,···,u8},and so the parametersui,i=1,2,···,240,correspond to 240 integral sections.According to the construction theorem in[19](Theorem(E8)),the values ofpi,qi,i=0,1,2,3 can be obtained fromui,i=1,2,···,8.

The similar proof can apply to the later case–a node curve(see[20]).

For the other two cases–the Mordell-Weil groups of fibrations related to the corresponding cubic pencils are,we note that by Lemma 5.2,not all the elements in the cubic pencil are smooth and then the conclusions follow from Theorem(E7),Theorem(E6)in[20]and[21].

The proof is complete.

6 Applications

Let us rewrite Theorem 1.4 in the following form.

Theorem 6.1(1)Given 8 points in general position in P2.If surfaceSis obtained by blowing-uppi,i=1,2,···,8,then there exist exactly 240(-1)-curves onS.

(2)Given 7 points in general position in P2.If surfaceSis obtained by blowing-uppi,i=1,2,···,7,then there exist exactly 56(-1)-curves onS.

(3)Given 6 points in general position in P2.If surfaceSis obtained by blowing-uppi,i=1,2,···,6,then there exist exactly 27(-1)-curves onS.

Proof(1) Given 8 pointsp1,p2,···,p8in general position.It is easy to construct a cubic pencilsH1+tH2with simple base pointsp1,p2,···,p8.Then,by blowing-up these base points,we can get a surfaceand 9 sectionsPi,i=1,2,···,9.By Theorem 1.1,E(K)E8.So the number of integral sections is 240.

Assume (P9)=(O).Then by blowing-down (P9) on,we obtain the surfaceS.Note that the(-1)-curves inSare reduced from the(-1)-curves or(-2)-curves on.If a(-1)-curve onSis reduced from a(-1)-curves on,then this(-1)-curve can’t intersect with(O)on,and so it is an integral section on.Hence the number of(-1)-curves onSis 240.On the other hand,by Lemma 3.1,the(-2)-curves onmust be irreducible components of reduced fibers.Since all the fibers are irreducible,the(-2)-curves never exist on.

(2)Given 7 points in general position in P2.Firstly,according to the construction in[22],there exists a cubic pencilsH1+tH2such thatH1andH2intersect properly atp0,p1,···,p6and at another 2-multiple pointp7.

Then,by blowing-up all the base points ofsH1+tH2,we can get a surface.The only reduced singular fiber isIII(orI2),and henceE(K)=by Theorem 1.1.Now assume(P′)=(O).Since Θv,0corresponds to the identity component,which intersects with the zero section(O)(see Figure 3 and the red fiber components there).By blowing down(P′)and Θv,1in turn,we obtainS.

Note that the(-1)-curves onSare reduced from the(-k)-curves on.We can obtain the number of(-1)-curves onSas follows.

Since a(-1)-curve must be a section(see Lemma 3.1),it just intersects with one of the singular fiber components.If a (-1)-curve onSintersects with (O) or Θv,0,then the intersection number will go up after contraction.If the(-1)-curves onSare reduced from the(-1)-curves on,then the(-1)-curves onSmust intersect with Θv,1.Since the norm of sections=2χ(S)+2(O,P)-=3/2,the number of such sections is 56(see[2]).

Now consider the(-1)-curves onSreduced from the(-k)-curves(k≥2)on.Since a(-k)-curve must be one component of a reducible singular fiber(see Lemma 3.1),and Θv,0is contracted onS,after two times of contracting,the self intersection number of Θv,1is a positive integral number.Hence,in this case,there is no(-1)-curves reduced from the(-k)-curves.

In conclusion,the number of(-1)-curves onSis 56.

(3)The number of(-1)-curves onSfor case(3)can be obtained similarly to case(2).Readers can refer to[4]and[22].

The proof is complete.

Remark 6.1We can also get some special fibrations for the cases(1)and(2)in Theorem 1.3.Whenpi=0,qj=0 for alliandj,the first equation in(1.2)becomesy2=x3+t5,which is a fibration over P1with two singular fibers.When allpi=0,andq0=q1=q2=q3=0,q4=1,the first equation in(1.3)becomesy2=x3+xt3+t4,which is a fibration over P1with three singular fibers.For more details,see[23].