Space-Time Legendre Spectral Collocation Methods for Korteweg-De Vries Equation

,

(School of Mathematics and Statistics, Henan University of Science and Technology,Luoyang 471000, China)

Abstract: A Legendre-Legendre spectral collocation scheme is constructed for Kortewegde Vries (KdV) equation on bounded domain by using the Legendre collocation method in both time and space, which is a nonlinear matrix equation that is changed to a nonlinear systems and can be solved by the usual fixed point iteration.Numerical results demonstrate the efficiency of the method and spectral accuracy.

Keywords: Korteweg-de Vries equation; Space-time Legendre spectral collocation method; Initial-boundary value problem

§1.Introduction

The Korteweg-de Vries (KdV) equation is to describe a peculiar water wave which shape and speed do not change as it travels, known as solitary waves.The traveling wave solution of the KdV equation verifies the solitary wave phenomenon.It shows that it is produced by the interaction of nonlinear effect and dispersion phenomenon, and has a soliton type solution [12].Hence, the study of the KdV equation has significant theoretical and application value.

Some numerical algorithms were proposed for solving KdV equation.For example,Cheng[3]used the Finite element method, Yu and Chen [11] provided the B-spline finite volume method.In Last 30 years, spectral methods have made many achievements in solving numerically partial differential equations [1,2,4,9,10].Some authors studied the Fourier spectral method [8] and the Chebyshev-Hermite spectral collocation method [5] to solve the KdV equation.Recently,Ma et al [7] considered the Legendre-Hermite space-time spectral collocation method for the initial value problem of the KdV equation.Based on the above ideas, we study the Legendre spectral collocation method for the initial-boundary value problem of the KdV equation.

The Legendre-Gauss-Lobatto nodes are used as collocation points in both time and space directions to construct the bivariate Lagrange interpolation approximation function and obtain the nonlinear equation.The high accuracy numerical solution of (1.1) can be obtained by simply fixed-point iteration.

§2.Interpolation polynomial and its differential matrix based on Legendre-Gauss-Lobatto integral nodes

LetLN(x)(x∈I=(-1,1)) be Legendre polynomial of orderN.x0=-1,xN=1 andxj(1≤j ≤N-1) are the roots of?xLN(x)=0.The Lagrange interpolation polynomial withxjas the interpolation node in [6]:

and thejorder differential matrix is the first order differential matrix to thejpower, which isD(j)=Dj.

Moreover,ψm(t) represents the basis function of the interpolation polynomial in the time direction, noting ?dl,m=?tψm(tl),tl(l=1,2,···,M) are the interpolation nodes in the time direction.We can derive a differential matrix element expression similar to (2.2).

§3.Legendre spectral collocation scheme for mixed problems of KdV equation

Letγ=ν=1 andμ=0.We can get the third order KdV equation

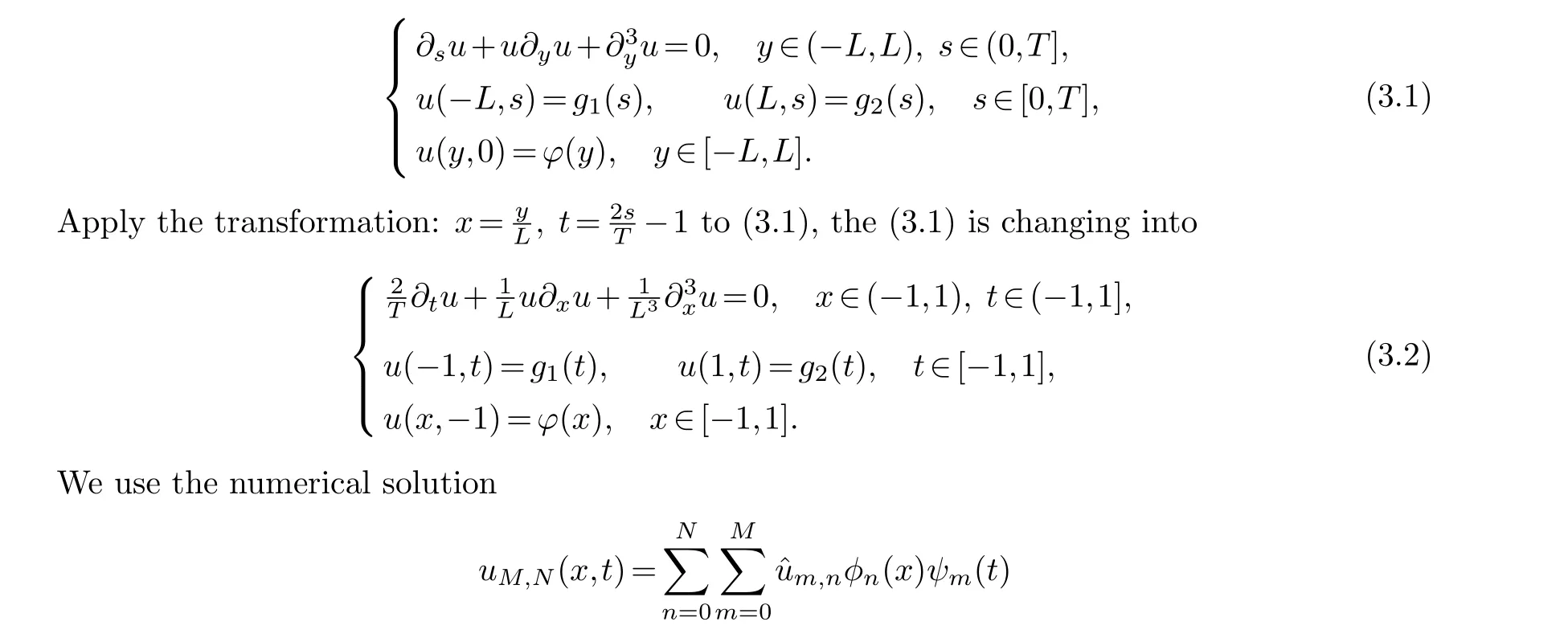
to approximate the solution of (3.2) and substitute it into (3.2) to obtain its spectral collocation schem

We can get

We can equivalently express (3.4) as

The operation “.?” is to multiply the elements at the corresponding positions of two matrixAandB.Let

The following equation can be obtained

§4.Numerical results

In actual computation, the (3.6) is transformed into a set of nonlinear systems, and its approximate solution is obtained by fixed-point iterative method.Let

whereκandx0are given parameters.We useL∞- error

to measure the numerical error.

Fig.1 shows the maximum errorEM,Nchanging withNin space direction withL=70,T=1 in (1.1),x0=20 in (4.2),M=8 in time direction, and differentialκ.The results show that the proposed scheme works well in space direction, and the parameterκhas a certain effect on the error.

Fig.1 L∞- errors with M=8, x0=-20, T=1.

Fig.2 is that the CPU spent time (seconds) asNchanging, which shows that the algorithm proposed in this paper has high efficiency.

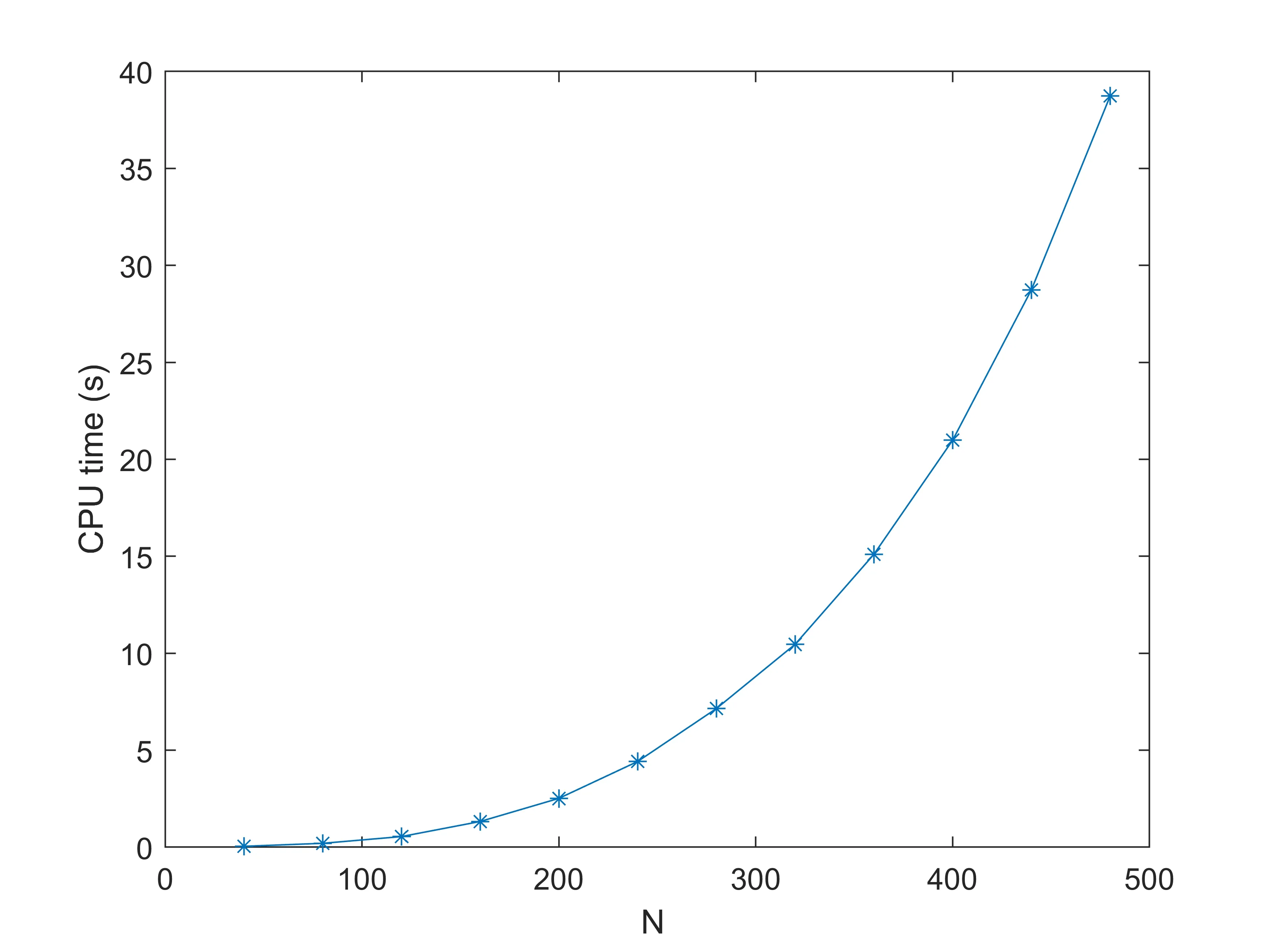
Fig.2 CPU elapsed seconds with M=8, x0=-20, T=1.

Fig.3 shows the maximum errorEM,Nvs.NwithL=70 in (1.1),κ=0.5,x0=2 in (4.2),andM=8 of time direction, which indicates that the algorithm of this paper works well when the parameterκis large.

Fig.3 L∞- errors with M=8, κ=0.5, x0=2, T=1.

Fig.4 plots the maximum errorEM,Nvs.NwithL=70 in (1.1),T=1,κ=0.3 in (4.2),M=8 and differentialx0, which shows that the selection of parameterx0has a certain influence on the error.

Fig.4 L∞- errors with M=8, κ=0.3, T=1.

Fig.5 shows maximum errorEM,Nvs.MwithL=70,T=1 in (1.1),κ=0.3,x0=-20 in(4.2) andN=430, which indicates that the algorithm of this paper also has spectral accuracy in time direction.

Fig.5 L∞- errors with N=430, κ=0.3, x0=-20, T=1

§5.Conclusion remarks

The Legendre-Gauss-Lobatto nodes are selected as spectral collocation points, and the KdV equation is changed to the nonlinear matrix equation.Simple iteration is used to solve the problem, and the Runge phenomenon is avoided.The numerical results demonstrate that the approximate solution agrees with the theoretical solution.

Although we only consider KdV equation in this work, the algorithm proposed in this paper can also be used to solve other nonlinear partial differential equations.