The Existence of Ground State Solutions for a Class of Sublinear KirchhoffEquations
(School of Science, Tianjin University of Technology and Education, Tianjin 300222, China)
Abstract: In this paper, we study a class of sublinear Kirchhoffequations:
Keywords: Ground state solutions; Sublinear term; Variational method; Kirchhoffequation
§1.Introduction
We study the following Kirchhoffequations:
wherea,b>0,N ≥3,V:RN →R, can be sign-changing, andf:RN×R→R.
Kirchhofftype problems were proposed by Kirchhoffin 1883 [11] as an extension of the classical D’Alembert’s wave equation for free vibration of elastic strings.Since the pioneering work of S.Bernstein[4]and S.I.Pohoˇzaev[18],there are huge literatures on the studies of the existence and behavior of solutions of Kirchhoffeuqation, see [1,2,6,9,10,13,14,17,20–23,25].Assume thatV ∈L∞(RN) and there existβ,R0>0 such thatV(x)≥βfor all|x|≥R0, Bahrouni [3]proved the existence of infinitely many solutions for Kirchhoffequation by using the symmetric Mountain Pass Theorem.In [12], Li and Zhong obtained infinity many weak solutions when the nonlinear termf(x,u) is only locally sublinear by a variant of the symmetric mountain pass lemma due to Kajikiya and Moser iteration method.In [7,24], the authors studied Kirchhoffequations with sublinear growth under different conditions.The difficulty for Kirchhoffproblem is proving compactness of PS sequence.However, the potential in [7] is a positive function which is different from ours.In [15,19], the results for Schr¨odinger-Poisson systems with sublinear growth are considered.Similar results can also be found in [5,8].
Assume that the following conditions hold:(V)V ∈LN/2(RN,R) satisfies‖V-‖N/2 Then problem(1.1)has a ground state solution with negative energy. Lemma 2.1.The functional I satisfies(PS)c condition for any c∈R. Proof.First, we show thatIis bounded from below.By H¨older inequality and Sobolev embedding, foru∈E, we have Next, we prove thatIsatisfies the (PS) condition.Assume that{un}n∈N?Eis a sequence such that{I(un)}n∈Nis bounded andI′(un)→0 asn→+∞.Consequently, by (2.1), there exists a constantC>0 such that Proof of Theorem 1.1.LetK={u∈E{0}|I′(u)=0}be the set of nontrivial critical point ofI, and define By Theorem 4.4 of [16], we getc?=infE I(u) is a critical value ofI, that is, there exists a critical pointu0∈Esuch thatI(u0)=c?.Finally, we show thatu0/=0. Letw ∈E{0}, we see that Since 0 We claim thatc=c?. Indeed, note thatK ?E, we havec≥c?. On the other hand, sinceu0is nontrivial critical point ofI, we obtain thatu0∈K, andc?=I(u0)≥c.Thus, we know thatc=c?=I(u0).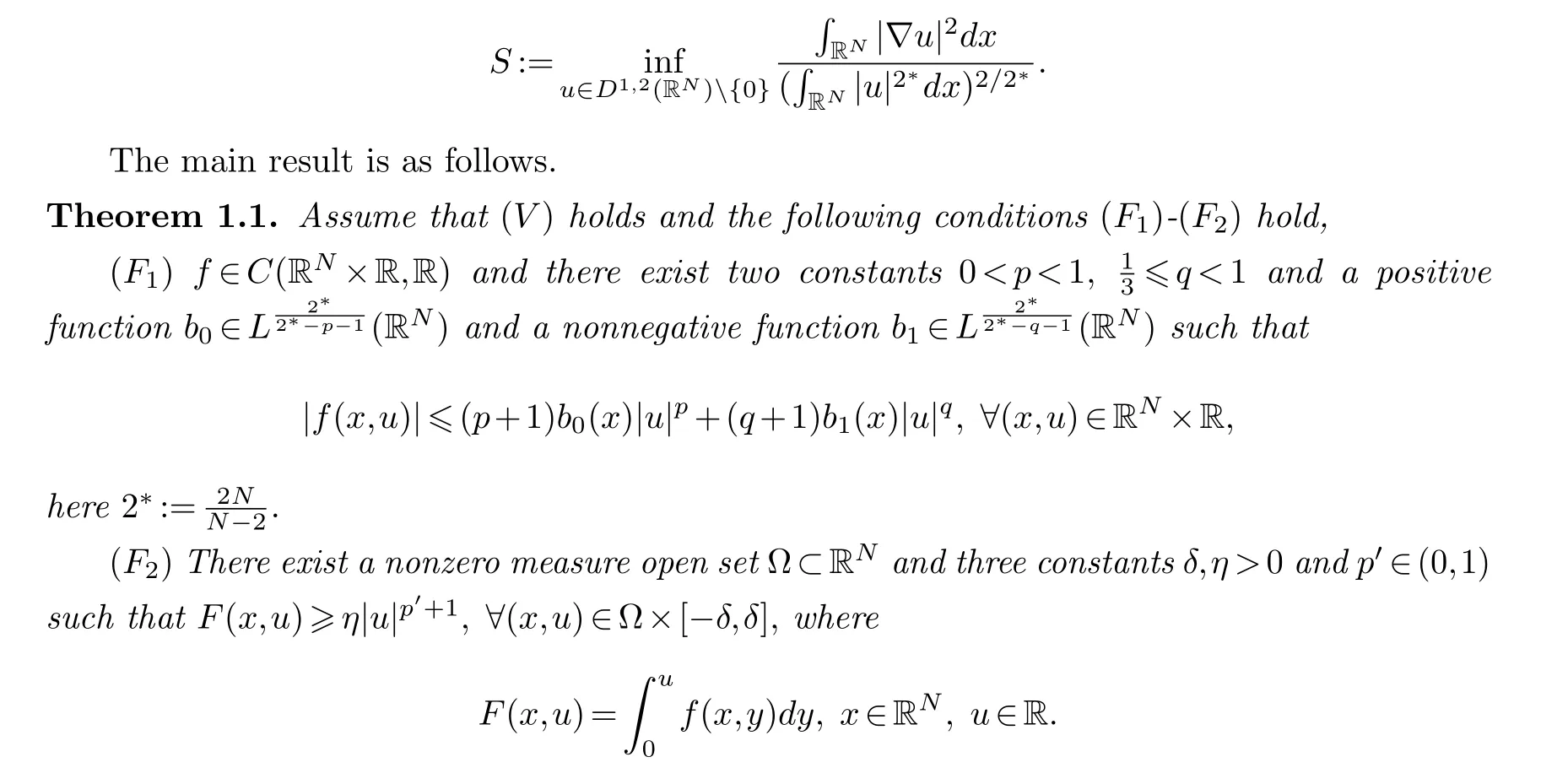
§2.Preliminary results



§3.Proof of Theorem 1.1
 Chinese Quarterly Journal of Mathematics2023年4期
Chinese Quarterly Journal of Mathematics2023年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- Exact Boundary Controllability for a 1-D Second-Order Quasilinear Hyperbolic System
- Singularity of Two Kinds of Four Cycle Graphs
- Initial Boundary Value Problem for Pseudo-Parabolic p-Laplacian Type Equation with Logarithmic Nonlinearity
- Construction of a Class of Gerstenhaber Algebras
- Subordination and Superordination Results for a Certain of Integral Operator Involving Generalized Mittag-Leffler Functions
- Competitive Equilibrium of Central Bank Digital Currency and Private Cryptocurrency: A Perspective of Regulatory
