三角形垂心的一個定理及其運用
2024-03-08 12:40江西省撫州市第二實驗學校344000洪海燕
中學數學研究(江西) 2024年3期
江西省撫州市第二實驗學校 (344000) 洪海燕
定理設ΔABC的垂心為H,外接圓半徑為R,則AH=2R|cosA|,BH=2R|cosB|,CH=2R|cosC|.


圖1
CH=2RcosC.
當ΔABC為鈍角三角形時,不妨設角A為鈍角,如圖2所示,易知AH=2Rcos(π-A)=-2RcosA,BH=2RcosB,CH=2RcosC.
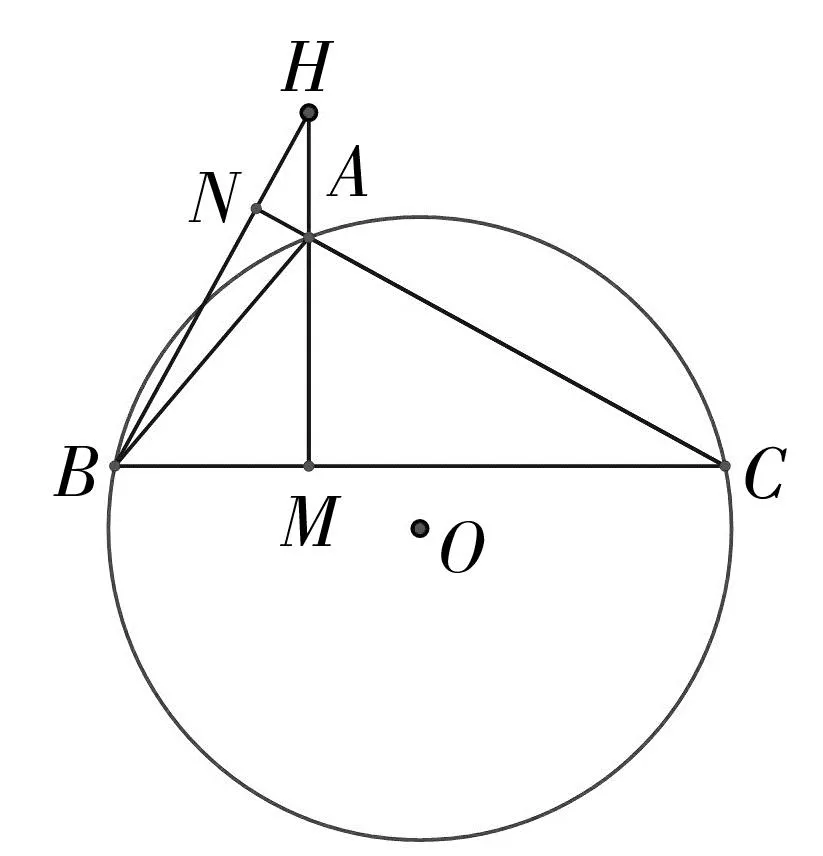
圖2
當ΔABC為直角三角形時,不妨設角A=90°,如圖3,可驗證定理的結論仍然成立.所以定理對任意ΔABC都成立.

圖3
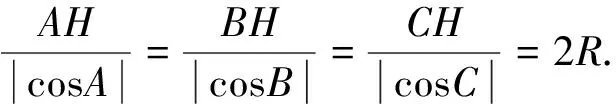
形式上與正弦定理類似.
以下略舉數例說明定理的應用.


例2 (三角形垂心與外心之間的關系定理)三角形任意一個頂點到垂心的距離,等于外心到該頂點對邊的距離的2倍.
證明:如圖4,已知H,O分別是ΔABC的垂心和外心,OM⊥BC于M,ON⊥AC于N,OK⊥AB于K.即要證:AH=2OM,BH=2ON,CH=2OK.

圖4

同理有BH=2ON,CH=2OK.
例3 設銳角ΔABC的外心與垂心分別為O,H,外接圓半徑與內切圓半徑分別為R,r,求證AH+BH+CH=2(R+r).
證明:如圖5,過外心O分別作OM⊥BC于M,ON⊥AC于N,OK⊥AB于K.由例2知AH+BH+CH=2(OM+ON+OK),故以下只要證明OM+ON+OK=R+r即可.
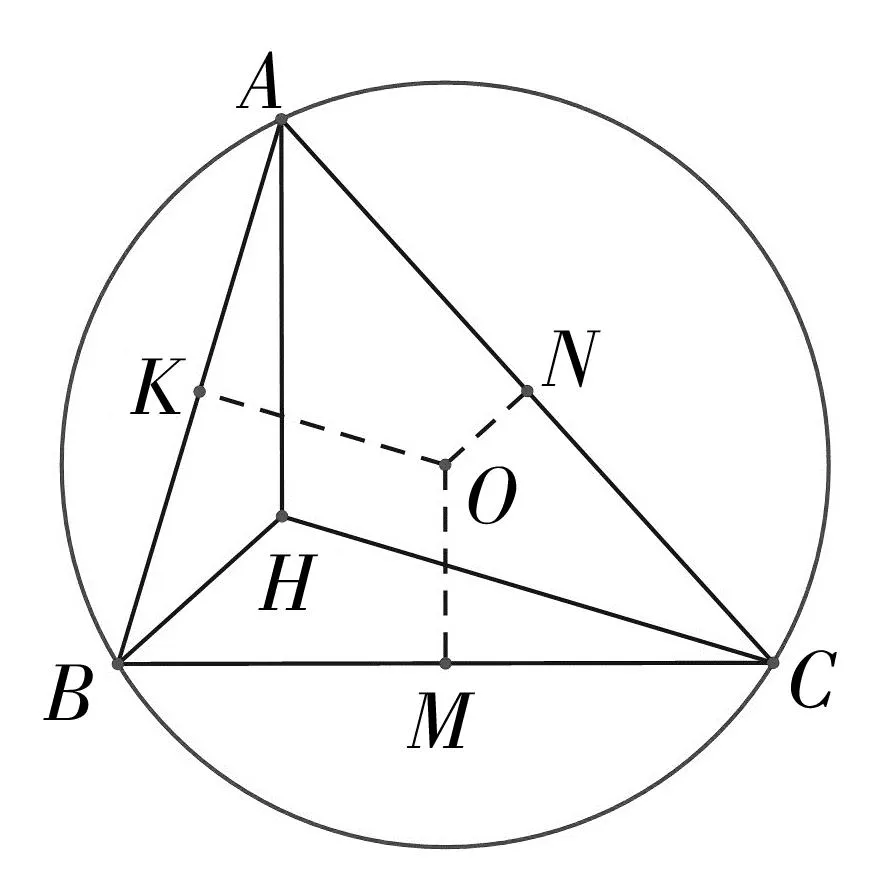
圖5
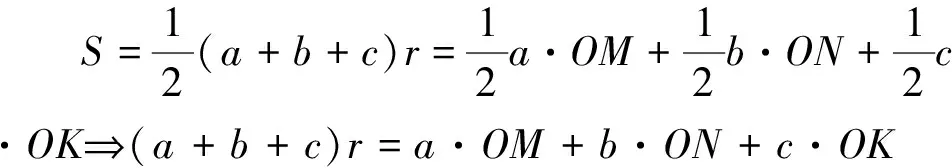
猜你喜歡
學校教育研究(2022年7期)2022-04-24
中學生數理化·高一版(2022年2期)2022-04-05
中等數學(2021年6期)2021-08-14
中等數學(2021年2期)2021-07-22
中等數學(2020年9期)2020-11-26
中學數學教學(2019年3期)2019-06-21
中等數學(2018年8期)2018-11-10
中等數學(2018年7期)2018-11-10
中學數學雜志(高中版)(2018年1期)2018-01-27
數學學習與研究(2017年13期)2017-07-21

