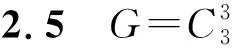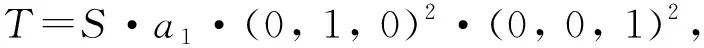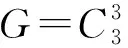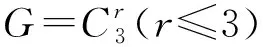初等3-群中表出達文波特常數的極小集
趙小越,吳雄華
(天津工業大學 數學科學學院,天津 300387)
0 引言
從20世紀60年代阿貝爾群上的零和問題開始被研究,近幾十年來取得了迅速發展[1-2].令G是一個加法有限阿貝爾群,由有限阿貝爾群基本定理,|G|=1或G?Cn1⊕…⊕Cnr,其中1 達文波特常數D(G)是零和理論的起點之一,也是本文的研究對象之一.達文波特常數是一個最小的常數t,使G上每個長度大于等于t的序列S都有非空的零和子列.令A(G)是G上所有極小零和序列構成的集合,B(G)是G上所有零和序列構成的幺半群,記G上空序列1為幺半群B(G)上的單位元.高維東等人為了統一表達零和不變量定義了dΩ(G)[3].對于Ω?B(G),定義dΩ(G)是一個最小的整數t,使G上每個長度大于等于t的序列S在Ω內都有子列.若這樣的t不存在,則令dΩ(G)=∞,因此1∈Ω時dΩ(G)=0.故在后文中,只討論Ω?B(G){1}的情況.文獻[4][5]繼續研究了dΩ(G)及其相關變量的零和問題. 是G0上的一個序列.序列中元素用符號· 連接,通常情況下可以省略.令 vg(S)是g在S上的重數; 若σ(S)=0,則稱S是一個零和序列; 若S沒有非空零和子列,則稱S是無零和序列; 對于g∈G0,若vg(T)≤vg(S),則稱T是S的一個子列,記作T|S; 若非空零和序列S的每個真子列都是無零和序列,則稱S是極小零和序列. 顯然空序列 1不是極小零和序列,因此A(G0)?B(G0){1}.若dΩ{S}(G)>dΩ(G),則稱序列S在Ω內是不可去序列.Ω是dΩ(G)=t的最小Ω當且僅當Ω中任意序列都是不可去序列. 引理2.1[4]設p是一個素數,當G是以下群時,有D(G)=M(G) : (1)r(G)≤2 ; (2)G是一個有限阿貝爾p-群. 引理2.2[3]令Ω,Ω′∈B(G){1} ,若Ω?Ω′,則dΩ′(G)≤dΩ(G) . 引理2.3Ω是dΩ(G)=D(G)的最小Ω當且僅當Ω上的每個序列S都在群G上存在一個D(G)長的序列W,且W所有的非空零和子列和S形式相同. 證明由文獻[4]中引理5.7顯然得到. 引理2.4G=C3⊕C3時A(G)是dΩ(G)=D(G)的最小Ω. 證明因為C3?Z3,下面對G=Z3⊕Z3展開證明.由Ωmin定義,Ωmin?A(G*),因此只需證A(G*)?Ωmin,即任意S∈A(G*)都有S∈Ωmin.由引理2.1,D(G)=5.顯然長度為D(G)的極小零和序列一定屬于Ωmin,所以任意長度為5的極小零和序列都屬于Ωmin,因此只需證任意S∈A(G*),|S|≤4,都有S∈Ωmin. 當S∈A(G*),|S|=1時,S只能為序列(0,0),令T=S·(0,1)2·(1,0)2,則T的零和子列只形同于S.即S∈A(G*),|S|=1,有S∈Ωmin. 當S∈A(G*),|S|=2時.若存在序列T,使T的零和子列只形同于(1,0)(2,0),那么也存在序列T′,使T′的零和子列只形同于(0,1)(0,2),稱這樣的性質為對稱性.由對稱性,只需討論以下三個極小零和序列,分別為 S1=(1,0)(2,0);S2=(1,1)(2,2);S3=(1,2)(2,1). 則存在 只含有形同于S1,S2,S3的極小零和序列.因此對于任意S∈A(G*),|S|=2,都有S∈Ωmin. 當S∈A(G*),|S|=4時,設S=a1·a2·a3·a4.由S∈A(G*),序列中有且僅有兩個線性無關元,設a1=(1,0),a2=(0,1) .若a3或a4=(1,0),則 S=(1,0)2(0,1)(1,2). 令T=S·(0,1) ,則T的零和子列只與S形同.若a3=a4≠a1≠a2,則 S=(1,0)(0,1)(1,1)2. 令T=S·(0,1),則T的零和子列只形同于S.此時不存在四個元素互不相同的情況.由對稱性和序列的無序性,長度為4的極小零和序列都屬于Ωmin. 綜上,任意S∈A(G*) ,|S|≤4,都有S∈Ωmin.G=C3⊕C3時A(G)是dΩ(G)=D(G)的最小Ω得證.該定理證畢. 若S∈A(G*)且|S|=1,則S只能為(0,0,0).令T=(0,0,0)(1,0,0)2(0,1,0)2(0,0,1)2,則T的極小零和子列只與S形同.所以長度為1的極小零和序列屬于Ωmin. 若S∈A(G*)且|S|=4,設S=a1·…·a4.由S∈A(G*),序列中至少有兩個線性無關元.若序列中僅有2個線性無關元,類似上述方法,由引理2.4存在極小零和子列只與S形式相同的序列.若序列中有3個線性無關元,設a1=(1,0,0) ,a2=(0,1,0),a3=(0,0,1),則S=a1·a2·a3·(2,2,2).令T=S·a1·a2·a3,則T的極小零和子列只與S形同.由對稱性,長度為4的極小零和序列都屬于Ωmin. 若S∈A(G*)且|S|=5,設S=a1·…·a5.由S∈A(G*),則S至少有2個線性無關元.若S中僅有2個線性無關元,設a1=(1,0,0),a2=(0,1,0),則a3,a4,a5可由a1,a2線性表出.類似上述方法,由引理2.4,存在極小零和子列只形同于S的序列.若序列中有3個線性無關元,令 a1=(1,0,0),a2=(0,1,0),a3=(0,0,1) 若a4或a5=aj,j∈[1,3],不妨設a4=(1,0,0).此時 S=(1,0,0)2(0,1,0)(0,0,1)(1,2,2). 令T=S·a2·a3,則T的極小零和子列只與S形同.若a4=a5≠aj,j∈[1,3].由S∈A(G*) 得 S=(1,0,0)(0,1,0)(0,0,1)(1,1,1)2. 令T=S·a1·a2,則T的極小零和子列只與S形同.若序列5個元素互不相同,只需討論以下兩種情況: S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(2,1,0),T=S·a4·(2,1,0); S=(1,0,0)(0,1,0)(0,0,1)(1,0,1)(1,2,1),T=S·a1·(1,2,1). 上述T的極小零和子列均只與它所對應的S形式相同.由對稱性和無序性,長度為5的極小零和序列都屬于Ωmin. 若S∈A(G*)且|S|=6,設S=a1·…·a6.由S∈A(G*),序列中有且僅有3個線性無關元,令 a1=(1,0,0),a2=(0,1,0),a3=(0,0,1). 若a4=a1=(1,0,0),a5=a2=(0,1,0),由S∈A(G*)有 S=(1,0,0)2(0,1,0)2(0,0,1)(1,1,2). 令T=S·(0,0,1),則T的極小零和子列只與S形式相同.若a4=a1=(1,0,0),討論以下兩種情況: S=(1,0,0)2(0,1,0)(0,0,1)(0,1,1)(1,1,1),T=S·(0,1,0); S=(1,0,0)2(0,1,0)(0,0,1)(0,1,2)(1,1,0),T=S·(0,0,1). 存在序列T,它的極小零和子列只形同于對應的S.若a4=a5≠a1≠a2≠a3,討論以下情況: S=(1,0,0)2(0,1,0)(0,0,1)(0,1,2)(2,0,1),T=S·(1,0,0); S=(1,0,0)2(0,1,0)(0,0,1)(0,1,1)(1,2,2),T=S·(0,1,0). 存在T的極小零和子列只與對應的S形式相同.若序列中6個元素互不相等,討論以下情況: S=(1,0,0)(0,1,0)(0,0,1)(1,1,0)(0,1,1)(1,0,1),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(1,1,0)(2,1,1)(2,0,1),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(1,1,2)(1,0,1)(0,1,2),T=S·(0,0,1); S=(1,0,0)(0,1,0)(0,0,1)(1,1,2)(1,2,2)(0,2,1),T=S·(0,1,0); S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(1,0,1)(1,1,2),T=S·(1,0,0); S=(1,0,0)(0,1,0)(0,0,1)(0,1,2)(1,0,2)(1,1,1),T=S·(0,0,1); S=(1,0,0)(0,1,0)(0,0,1)(1,2,2)(0,2,1)(1,1,2),T=S·(0,1,0); S=(1,0,0)(0,1,0)(0,0,1)(1,2,2)(2,1,2)(2,2,1),T=S·(2,1,1). 上述T的極小零和子列均只與它所對應的S形式相同.由對稱性和無序性,長度為6的極小零和序列都屬于Ωmin. 證明r=1時,G=C3,顯然成立.由引理2.4和引理2.5,定理顯然成立.該定理證畢.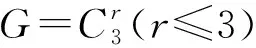
1 定義及符號介紹
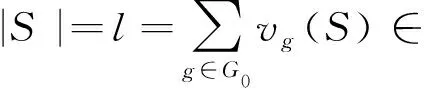

2 定理的證明