窮根究底,“增解”何來?
2024-03-08 12:38福建省泉州市第七中學362000賴呈杰林景芳
中學數學研究(江西) 2024年3期
福建省泉州市第七中學 (362000) 賴呈杰 林景芳
在解三角形問題中,根據條件建立方程計算線段長度或角度時經常會產生“增解”問題.本文筆者以2023年全國新高考Ⅰ卷17為例,明晰“增解”來源,理清“舍根”方法,并提出避免產生“增解”的幾種策略,希望對讀者有所幫助.
1 問題起源
(2023年全國新高考Ⅰ卷17)已知在△ABC中,A+B=3C,2sin(A-C)=sinB.
(1)求sinA;(2)設AB=5,求AB邊上的高.
分析:第(1)小題考查三角恒等變換求三角函數值,第(2)小題可通過等面積法求AB邊上的高.即將問題轉化為“三角形中,已知兩個內角與一條邊,求其他邊長”.即求b.
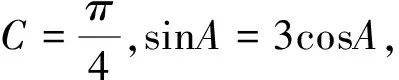

圖1
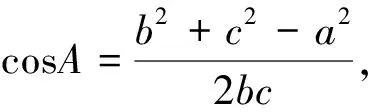


可以發現,以上三種思路均采用余弦定理,思路2卻產生了增解.原因在哪里?如何舍去增解?已知“兩邊一對角”情形下,選擇哪個角使用余弦定理最佳?
2 為何有增解
2.1 “增解”的幾何解釋
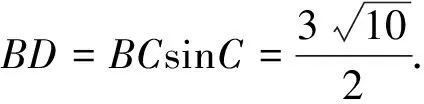

圖2
2.2 “增解”的代數說明
已知a,c和角C,對角C使用余弦定理,并將其整理為關于b的一元二次方程b2-2abcosC+a2-c2=0(*).判別式Δ=(2acosC)2-4(a2-c2),化簡得Δ=4(c2-a2sin2C)=4(c+asinC)(c-asinC),則①若方程(*)有兩個不等的正數解,則該三角形有兩解;②若方程(*)有一個正數解,則該三角形有一解;③若方程(*)無解或只有負數解,則該三角形無解.
限于篇幅,僅證明①.

3 如何舍去增解
在△ABC中,由正弦定理可知,a>b>c?A>B>C,可以通過對角的大小比較得到邊的大小關系.對于思路2中產生的增解,有以下常用方法舍去.



4 避免產生增解的策略
策略1 對較大角使用余弦定理

策略2 運用射影定理
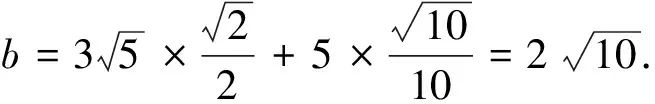
策略3 運用正弦定理

解三角問題中,只要甄別好條件,運用余弦定理來辨析三角形解的個數也是可行的.由此,可幫助學生面對此類試題時做好決策,做到胸有成竹,事半功倍!
猜你喜歡
中學生數理化(高中版.高二數學)(2020年11期)2020-12-14
中學生數理化(高中版.高考數學)(2020年10期)2020-10-27
河北理科教學研究(2020年1期)2020-07-24
中學生數理化·七年級數學人教版(2019年9期)2019-11-25
數學年刊A輯(中文版)(2018年4期)2019-01-08
智富時代(2017年4期)2017-04-27
智富時代(2017年4期)2017-04-27
中學生數理化·七年級數學人教版(2016年9期)2016-12-07
中學生數理化·七年級數學人教版(2016年8期)2016-12-07
文山學院學報(2012年6期)2012-03-25

