正方形背景下的等腰直角三角形問題

廣東省中山市橫欄中學(528478) 齊彩霞

1 教學設計過程

1.1 題目設計

如圖1,已知,正方形ABCD中,E為線段AD上一動點,F為DC延長線上一動點,若AE=CF,ΔBEF為等腰直角三角形嗎?

1.1.1 主題設計意圖

此題圖形簡潔,正方形與等腰直角三角形以及全等相融合,通過轉角可形成等腰直角三角形,在這種基本圖形背景下還可發散學生思維,生成更多有效學習經驗.

問題1 同學們通過證明ΔAEB～=ΔBCF,再轉邊轉角得證原題1,你還能由此題聯想到其他問題嗎? 比如,條件結論是否可以互換,在原題的基礎上還可以引發哪些新問題?

1.2 變式1,變式2 題目呈現

變式1 如圖2,已知,正方形ABCD中,E為線段AD上一動點,F為DC延長線上一動點,若∠EBF=90°,請問AE=CF嗎?

設計意圖在問題1 的思考下,學生應該可以順其自然想到變式1,或者其他類似變式,這種連貫的思考,更能引發學生潛在的動力,提高學習的興趣,當然也為進一步的探索變形做準備.

問題2 同學們在變式1 與原題1 證明中其實都是采用全等,兩題其實“換湯不換藥”,有了前面的經驗,變式2 還可以有哪些改編? 比如E,F點一定要在正方形邊上嗎? 如果在其他位置,結論是否成立?

變式2 如圖3,正方形ABCD中,以點B為直角定點作等腰直角三角形BEF,請問AE=CF嗎?

設計意圖對比變式1,弱化了“在正方形邊上”的條件,強化了“等腰”條件,這樣的變形學生們可以接受,也能領會深層的舉一反三,更容易激發學生的內驅力,學生也會覺得利用上題的知識可以反饋到這道題中,但又不會像單純的“無腦換數”變式那樣無趣.

1.3 變式3,變式4 題目呈現

變式3 如圖4,點E為正方形ABCD外一點,∠BEC=45°,連接AE,

(1)求∠AEB的度數.(2)求證:AE+CE=

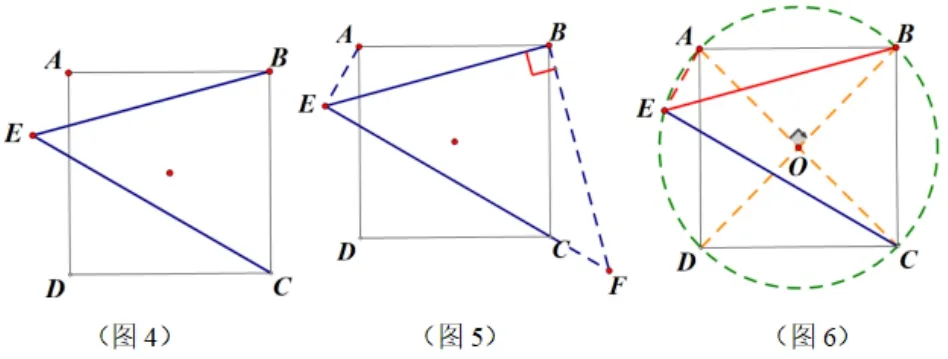
設計意圖變式3 其實是變式2 的拔高,前面3 題還是學生能思考,能突破,變式3 的條件更少,但仍然與前3 題保持緊密聯系,學生可以敏銳的發現“45°”的特別之處,至于該如何處理,會引發學生的“頭腦風暴”,充分調動學生的求知欲,再通過小組討論,上臺展示的方法會更好地引起學生的共鳴,從而把此題的思考方法真正由學生教給學生.

解法補充法一:根據變式3 于2 的共性45°,學生可猜測通過以BE為直角邊構造等腰直角三角形((如圖5),再由全等證明∠AEB=∠BFA=45°.

法二:∠BEC=45°,相當于“定弦定角問題”,如圖6,以正方形中心O為圓心,OA為半徑構造圓,∠BEC即為圓周角,由同弧所對的圓周角相等,故∠AEB=∠BEC=45°

變式4 如圖7,在原題1 的條件下,正如果方形的邊長為4,連接BD,取EF的中點M,連接CM.

(1)是否有∠EBD=∠EFD?

(2)CM是否為線段BD的垂直平分線?

(3)點M的軌跡是?點M的軌跡長是多少?

(4)若DE=2,則CM=?

設計意圖變式1-3,層層深入,學生們會有一種意猶未盡的快感,這種求知欲會讓學生自覺對原題進一步探索,因此變式4 是筆者在原題1 的基礎上引申出其他的思考,關鍵在于“對角線BD”的出現,對角線有很多很好的特征,利用對角線的“平分對角,對角線互相垂直”,可以引發變式4 的4 小問思考,也可以突破學生的思維.

解法補充學生講解中:第(1)問可把圖中的所證角抽離出(如圖8),通過圖中的等角,可得出所求角相等.第(2)問:部分學生遺忘了“垂直平分線的判定”從而難以解題,因此可通過回顧垂直平分線的判定,找到所證垂直平分線上兩點,去證明兩點都在垂直平分線上:即求證CB=CD,MD=MB,即可得證.第(3)問,即在第(2)問的基礎上拔高,其實已經知道M在BD的垂直平分線上,故關鍵在于M的起始位置,即可得證.第(4)問,學生主要想把DE的長度進行轉移,通過轉化已知長度把CM與已知長度聯系起來,由于“M”中點的特殊性,可聯系“直角三角形斜邊中線或中位線”轉移,這里“中位線”比較適合(如圖9).

2 作業設計

變式5 (如圖10)正方形ABCD中,以B為直角頂點作等腰直角三角形BEF,其中BE=BA,M為線段EF的中點,連接CM;

(1)點M的軌跡是?CM長度的最小值?

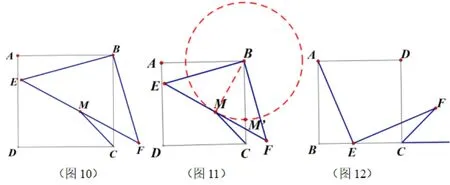
設計意圖前面都是點E在正方形邊上,或在外部,自然會思考在正方形內部會發生什么變化,如果只是“以B為直角頂點作等腰直角三角形BEF”,點E的位置太一般,考慮的價值不夠高,故強化:BE=BA,相當于ΔBAC繞著點B旋轉,隨著ΔBAC的位置不同,此時M也會隨EF的變化而變化,CM的長度也在改變,自然想到最值問題,學生可以根據點M的特殊性求解(如圖11).

變式6 (如圖12)正方形ABCD中,E為線段BC上任意一點,連接AE,過點E作AE的垂線交正方形外角的平分CF于點F.求證AE=AF

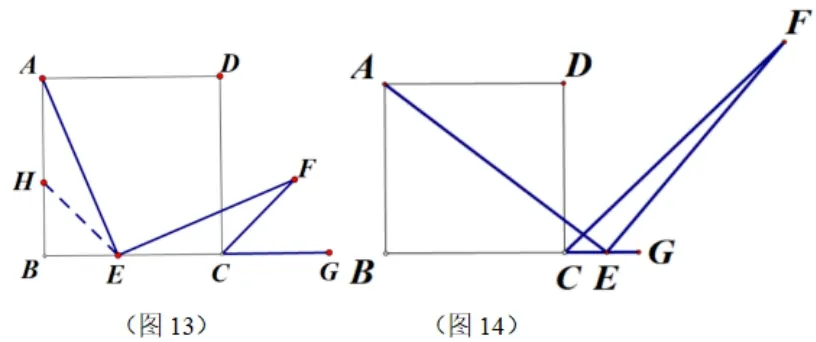
變式7 (如圖14)如果把“E為線段BC上一動點”改為“如果點E為BC延長線(除點C外)的任意一點,其他條件不變,求證AE=EF”

問題8 你還能想到那些正方形背景下的等腰直角三角形相關問題,解決此類問題的基本途徑是什么? 在解題和改編題目中你有什么啟發與收獲.

設計意圖變式6,7 看似與1-5 題聯系不大,但“CF”是直角三角形的角平分線,由此45 度出現,學生可以聯想到“等腰直角”的特殊性質,學生觀察到三角形AEF的等腰直角屬性,可猜測通過全等證明對應邊相等,而AE,FE在哪兩個全等三角形中呢? 優生可以猜想到固定ΔCEF,構造與之全等且含AE邊的三角形,故在圖中可在BA上截取BH=BE(如圖13).易證AE=FE.問題8 是開發性問題,中低層學生可以簡單概括本節課的知識點,方法等,優生可以進一步拓展正方形背景下的等腰直角三角形問題,領會一題多變,從不同角度發現問題,解決問題的方法.

3 反思與小結

“正方形為背景下的等腰直角三角形問題”是比較常見的綜合幾何題,課堂上如果偶爾講一題效果不太顯著.講的太深了學生也很難接受,因此合理高效的設計尤為重要,筆者認為題目的選取應由淺入深,由表及里,層層遞進,一題多解,多解歸一,一題多變,多題歸一.一題多解不是僅僅追求解法多,更要通過解法發現問題的你本質,才是真正的理解題目的內涵,即題目的解法要有意義.而在一題多變中問題與問題的串聯中應環環相扣,聯系緊密,更容易激發學生的內驅力.在題型講解過程中教師要學會把課堂的主人還給學生,給學生充分討論與思考時間,每一道題不僅僅是講解題過程,更多的是分析,思考,總結.學生的總結往往站在學生的角度,他們的理解和發現可能會更精彩也更容易被學生所接受,在一道題的講解中還要引導學生挖掘更多有價值的信息,發散思維.比如原題中還能求出哪些長度,角度,是否可以證明等邊,等角,長度間的關系等.這些連貫易發現的問題,學生既容易提出問題,也容易理解思考.總之,教學本就是一個探索的過程,更是一個發現的過程,教師需要關注學生的學習背景,了解學生的知識理解程度和知識盲區,更要引導學生如何高效地學習,同時教師也要積極地提升自身的教學能力與自我修養.